
Consider the following linear programming problem:
Maximize \[12X + 10Y\]
Subject to: \[\begin{array}{l}
4X + 3Y \le 480\\
2X + 3Y \le 360\\
all\,variables \ge 0
\end{array}\]
Which of the following points \[\left( {X,Y} \right)\] could be a feasible corner point?
A) \[\left( {40,48} \right)\]
B) \[\left( {120,0} \right)\]
C) \[\left( {180,120} \right)\]
D) \[\left( {30,36} \right)\]
E) None of these
Answer
563.4k+ views
Hint:
Here we will firstly take the first constraint equation and find the points from which the line is passing. Then we will take the second constraint equation and find the points from which this second line is passing. Then we will plot these lines in a Cartesian plane and show the feasible region. Then we will simply choose the required corner points of the feasible region.
Complete Step by step Solution:
The equation to maximize is \[12X + 10Y\].
Given constraints, the equations are \[4X + 3Y \le 480,2X + 3Y \le 360\].
Firstly we will plot these lines on the Cartesian plane.
So we will take the first equation i.e. \[4X + 3Y \le 480\] and find the points from where the line passes. Therefore, we get
Substitute \[X = 0\] in the equation, we get \[3Y = 480\] by solving this we get \[Y = 160\]. Hence the point is \[\left( {0,160} \right)\].
Substitute \[Y = 0\] in the equation, we get \[4X = 480\] by solving this we get \[X = 120\]. Hence the point is \[\left( {120,0} \right)\].
Therefore, the line \[4X + 3Y \le 480\] passes through the points \[\left( {0,160} \right)\], \[\left( {120,0} \right)\].
Now we will take the second equation i.e. \[2X + 3Y \le 360\] and find the points from where the line passes. Therefore, we get
Substitute \[X = 0\] in the equation, we get \[3Y = 360\] by solving this we get \[Y = 120\]. Hence the point is \[\left( {0,120} \right)\].
Substitute \[Y = 0\] in the equation, we get \[2X = 360\] by solving this we get \[X = 180\]. Hence the point is \[\left( {180,0} \right)\].
Therefore, the line \[2X + 3Y \le 360\] passes through the points \[\left( {0,120} \right)\], \[\left( {180,0} \right)\].
Now we will plot these lines on the Cartesian plane and shade the feasible region. Therefore, we get
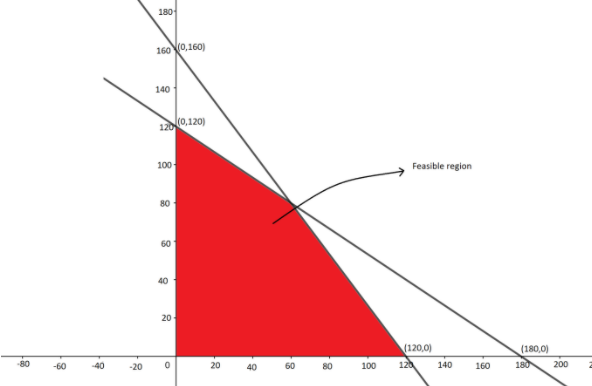
We can clearly see that the corner points of the feasible region are \[\left( {0,120} \right)\] and \[\left( {0,120} \right)\].
So, option B is the correct option.
Note:
Feasible region is the search space or the solution space where the value of the objective function is optimal. Maximum and the minimum value of the objective function are generally at the corner points of the feasible region. While calculating the points we have to put the value of each of the variables as zero to find the value of the points on the axis from which the line is passing. We should know the meaning of this sign \[ \le \] that it means the region is toward the origin of the Cartesian plane and for the sign \[ \ge \] means the region is away from the origin of the Cartesian plane.
Here we will firstly take the first constraint equation and find the points from which the line is passing. Then we will take the second constraint equation and find the points from which this second line is passing. Then we will plot these lines in a Cartesian plane and show the feasible region. Then we will simply choose the required corner points of the feasible region.
Complete Step by step Solution:
The equation to maximize is \[12X + 10Y\].
Given constraints, the equations are \[4X + 3Y \le 480,2X + 3Y \le 360\].
Firstly we will plot these lines on the Cartesian plane.
So we will take the first equation i.e. \[4X + 3Y \le 480\] and find the points from where the line passes. Therefore, we get
Substitute \[X = 0\] in the equation, we get \[3Y = 480\] by solving this we get \[Y = 160\]. Hence the point is \[\left( {0,160} \right)\].
Substitute \[Y = 0\] in the equation, we get \[4X = 480\] by solving this we get \[X = 120\]. Hence the point is \[\left( {120,0} \right)\].
Therefore, the line \[4X + 3Y \le 480\] passes through the points \[\left( {0,160} \right)\], \[\left( {120,0} \right)\].
Now we will take the second equation i.e. \[2X + 3Y \le 360\] and find the points from where the line passes. Therefore, we get
Substitute \[X = 0\] in the equation, we get \[3Y = 360\] by solving this we get \[Y = 120\]. Hence the point is \[\left( {0,120} \right)\].
Substitute \[Y = 0\] in the equation, we get \[2X = 360\] by solving this we get \[X = 180\]. Hence the point is \[\left( {180,0} \right)\].
Therefore, the line \[2X + 3Y \le 360\] passes through the points \[\left( {0,120} \right)\], \[\left( {180,0} \right)\].
Now we will plot these lines on the Cartesian plane and shade the feasible region. Therefore, we get

We can clearly see that the corner points of the feasible region are \[\left( {0,120} \right)\] and \[\left( {0,120} \right)\].
So, option B is the correct option.
Note:
Feasible region is the search space or the solution space where the value of the objective function is optimal. Maximum and the minimum value of the objective function are generally at the corner points of the feasible region. While calculating the points we have to put the value of each of the variables as zero to find the value of the points on the axis from which the line is passing. We should know the meaning of this sign \[ \le \] that it means the region is toward the origin of the Cartesian plane and for the sign \[ \ge \] means the region is away from the origin of the Cartesian plane.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




