Question

Consider an infinite ladder network shown in figure. A voltage is applied between the points $A$ and $B$ . If the voltage is halved after each section, find the ratio of $\dfrac{{{R_1}}}{{{R_2}}}$ . Suggest a method to terminate if after a few sections without introducing much error in its attenuation.

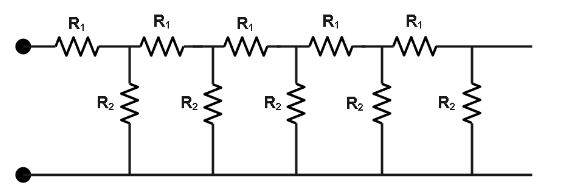
Answer 1

Hint: To solve this question, one must have a good concept of series and parallel combination. Here firstly we have assumed the net equivalent resistance as $R$ and then proceed accordingly. And it is given that the voltage is halved after each section. So, we must mention carefully and solve by applying series and parallel combinations.Net resistance of a series combination is given by,
${R_{eq}} = {R_1} + {R_2} + \cdot \cdot \cdot \cdot \cdot \cdot $
Net resistance of a parallel combination is given by,
${R_{eq}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$

Complete step by step answer:
Let us assume the equivalent resistance of the given circuit is $R$ . As we can see the circuit is infinitely long, so removing the loop from the circuit will not be affecting the equivalent resistance of the given circuit. So, the new circuit will become:

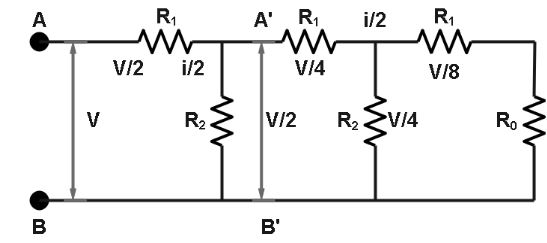
Let us assume the voltage across $AB = V$ then voltage across $A'B' = \dfrac{V}{2}$
Voltage across ${R_2} = \dfrac{V}{2}$.
Now applying the Kirchhoff’s law, we can say that the voltage across ${R_1}$ ​is
$V - \dfrac{V}{2} = \dfrac{V}{2}$
And
${R_1}i = {R_2}\dfrac{i}{2}$
$\Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{1}{2}$

The equivalent resistance of the given infinite ladder between $A$ and $B$ becomes independent of the units in between. It means, if we remove all the resistances, other than terminal resistance ${R_0}$ , the equivalent resistance across $A$ and $B$ should also be ${R_0}$.So, the total resistance of ${R_0}$ and ${R_2}$ is
$R' = {R_0} = {R_1} + \dfrac{{{R_0}{R_2}}}{{{R_0} + {R_2}}}$

As ${R_1}$ is in series combination with it, so the net equivalent resistance between $A$ and $B$ is:
${R_0} = {R_1} + \dfrac{{{R_0}{R_2}}}{{{R_0} + {R_2}}}$
Now solving for ${R_0}$ we will get the following,
${R_0} = \dfrac{{{R_1}}}{2}\left( {1 + \sqrt {\left( {1 + \dfrac{{4{R_2}}}{{{R_1}}}} \right)} } \right)$
Thus, we can conclude that the circuit may terminate after a few sections if the resistance ${R_0}$ is connected in parallel as shown above.

Hence, the ratio $\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{1}{2}$.

Note: We cannot find the equivalent resistance of the infinite ladder network by solving the equivalent resistance of every loop given in the circuit. You must always assume that the equivalent resistance of the network is $R$ then you can easily solve the question.And you must mention every point in the diagram while solving, then it will be easier to solve.