Question

Consider an ellipse having major axis and minor axis parallel to x-axis and y-axis respectively. Its foci S and S’ one $ (2,\,1)\,\,and\,\,(4,\,1) $ and a line $ x + y = 9 $ is tangent to this ellipse at point P.
1.) Eccentricity of ellipse is:
a) $ \dfrac{1}{{\sqrt {12} }} $
b) $ \dfrac{1}{{\sqrt {13} }} $
c) $ \dfrac{1}{2} $
d) None

2.) Length of major axis is:
a) $ \sqrt {13} $
b) $ 2\sqrt {11} $
c) $ \sqrt {52} $
d) $ 2\sqrt {12} $

Answer 1

Hint: To solve this problem we first calculate lengths of perpendicular distance from given foci, as the product of perpendicular distance from foci is equal to square of length of minor axis. After this we calculate distance between two foci as it is always equal to $ '2ae' $ . Using two equations so formed we get the value of eccentricity and hence length of major axis.
Distance formula between two points: $ \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $

Complete step-by-step answer:
Let consider an ellipse whose major and minor axis are parallel to x-axis and y-axis.
And let ‘a’ and ‘b’ are semi major and minor axis of ellipse.

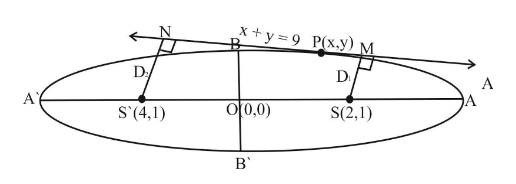
Also, foci of ellipse are given as $ (2,\,1)\,\,and\,\,(4,\,1) $ and a line $ x + y = 9 $ is tangent to ellipse at any point P.
Since, we know that the product of perpendicular distance from the foci on tangent line is equal to square of semi major axis.
 $ {D_1}\, \times {D_2}\, = \,{b^2} $ , where $ {D_1}\,and\,\,{D_2} $ perpendicular distance from foci to tangent line and ‘b’ are is length of semi major axis of ellipse.
Now, calculating $ {D_1}\,and\,\,{D_2} $ :
 $
  {D_1} =
   {\dfrac{{2 + 1 - 9}}{{\sqrt {1 + 1} }}}
  \\
   \Rightarrow {D_1} =
   {\dfrac{{ - 6}}{{\sqrt {1 + 1} }}}
  \\
   \Rightarrow {D_1} = \dfrac{6}{{\sqrt 2 }} \;
  $
Also,
 $ {D_2} =
   {\dfrac{{4 + 1 - 9}}{{\sqrt {1 + 1} }}}
 $
 $ \Rightarrow {D_2} =
   {\dfrac{{ - 4}}{{\sqrt 2 }}}
 $
 $ \Rightarrow {D_2} = \dfrac{4}{{\sqrt 2 }} $
Using above calculated values of $ {D_1}\,and\,\,{D_2} $ in above mentioned formulas we have
 $
  \left( {\dfrac{6}{{\sqrt 2 }}} \right) \times \left( {\dfrac{4}{{\sqrt 2 }}} \right) = {b^2} \\
   \Rightarrow \dfrac{{24}}{2} = {b^2} \\
   \Rightarrow {b^2} = 12 \\
  or \\
  b = 2\sqrt 3 \\
  $
Also, we know that distance between foci of an ellipse is equal to ‘ $ 2ae' $ , where ‘a’ is length of semi major axis and ‘e’ is eccentricity of an ellipse.
Therefore,
  $
  \sqrt {{{\left( {4 - 2} \right)}^2} + {{\left( {1 - 1} \right)}^2}} = 2.a.e \\
   \Rightarrow \sqrt 4 = 2.a.e. \\
   \Rightarrow 4 = 4a.e. \\
   \Rightarrow ae = 1 \;
  $
Now, squaring both side we have
 $ {e^2} = \dfrac{1}{{{a^2}}} $
Also, we know that there is a relation between eccentricity and minor, major axes. Which is given as
 $ {e^2} = \left( {1 - \dfrac{{{b^2}}}{{{a^2}}}} \right) $
Substituting above calculated values in above formed equation.
 $
  {e^2} = \left( {1 - \dfrac{{12}}{{1/{e^2}}}} \right) \\
   \Rightarrow {e^2} = 1 - 12{e^2} \\
   \Rightarrow {e^2} + 12{e^2} = 1 \\
   \Rightarrow 13{e^2} = 1 \\
   \Rightarrow {e^2} = \dfrac{1}{{13}} \\
   \Rightarrow e = \dfrac{1}{{\sqrt {13} }} \;
  $
Hence, from above we see that the eccentricity of the given ellipse is $ \dfrac{1}{{\sqrt {13} }} $ .
Therefore, from given four options for problem 1.) the correct option is (b).
Now, to find the length of the major axis.
From above we have a relation which is
 $ {e^2} = \dfrac{1}{{{a^2}}} $
Or
 $ {a^2} = \dfrac{1}{{{e^2}}} $
Substituting value of ‘e’ from above we have:
 $
  {a^2} = \dfrac{1}{{{{\left( {1/\sqrt {13} } \right)}^2}}} \\
   \Rightarrow {a^2} = 13 \\
   \Rightarrow a = \sqrt {13} \;
  $
Where, ‘a’ is the length of the semi major axis of ellipse.
Therefore, length of major axis of ellipse is given as = $ 2a $
Hence, length of major axis = $ 2\sqrt {13} $ or we can write it as $ \sqrt {52} $

So, the correct answer is “Option 2 AND D”.

Note: Ellipse is a symmetrical figure. So, while calculation we can consider either ‘a’ or ‘b’ as major and minor axis or vice-versa result remains the same. Which implies that while using the eccentricity formula of major axis of ellipse or minor axis of ellipse wouldn’t make an effect on calculation and hence on result.