Question

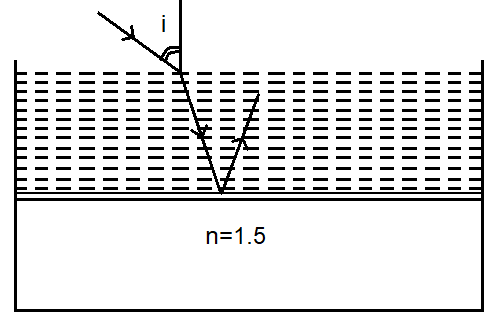
Consider a tank made of glass (refractive index $ 1.5 $ ) with a thick bottom. It is filled with a liquid of refractive index $ \mu $ . A student finds that, irrespective of what the incident angle $ i $ (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarized. For this to happen, the minimum value of μ is

(A) $ \dfrac{3}{{\sqrt 5 }} $
(B) $ \dfrac{5}{{\sqrt 3 }} $
(C) $ \sqrt {\dfrac{5}{3}} $
(D) $ \dfrac{4}{3} $

Answer 1

Hint: For finding out the minimum value of the refractive index, we need to use the relation between Brewster angle and the critical angle which is given as $ sin{\text{ }}c < sin{\text{ }}{i_{b\;}} $ . Brewster angle is an angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection.

Formula used:
 $ sin{\text{ c}} < sin{\text{ }}{i_{b\;}} $
 $ \
  sin90 = \mu \sin c \\
   \Rightarrow sinc = \dfrac{1}{\mu } \\
 $
Where, the critical angle be $ {\text{ c}} $ , the Brewster angle be $ {\text{ }}{i_{b\;}} $ , $ {\text{ }}\mu $ is the refractive index.

Complete step by step solution:
Let us consider the critical angle be c, the Brewster angle be ib.
The relation comes between the critical angle and the Brewster angle is,
 $ sin{\text{ }}c < sin{\text{ }}{i_{b\;}} $
For the ray travelling from air to liquid,
 $ sin90 = \mu \sin c $
Now the value of $ sin90 $ is 1 so we get
 $ sinc = \dfrac{1}{\mu } $
Since, we know that,
 $ \tan {i_b} = {\mu _{{0_{rel}}}} $
And,
 $ sin{\text{ }}c < sin{\text{ }}{i_{b\;}} $
Then substituting the values in the equation we get,
 $ \Rightarrow \dfrac{1}{\mu } < \dfrac{{1.5}}{{\sqrt {{\mu ^2} + {{(1.5)}^2}} }} $
Thus, after simplification, we get,
 $ \Rightarrow \mu < \dfrac{3}{{\sqrt 5 }} $
Hence, the correct answer is option A.

Note:
There are numerous applications of Brewster angle in real life. It includes,
-Polarized sunglasses use the principle of Brewster's angle to reduce glare from the sun reflecting off horizontal surfaces such as water or road.
-Photographers use the same principle to remove reflections from water so that they can photograph objects beneath the surface.
-Brewster angle prisms are used in laser physics. The polarized laser light enters the prism at Brewster's angle without any reflective losses.
-In surface science, Brewster angle microscopes are used in imaging layers of particles or molecules at air-liquid interfaces.