Question

Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ. The phase difference between the ray of reflected by the top surface of the glass and bottom surface is
A. \[\dfrac{4\pi d}{\lambda }{{\{1-\dfrac{1}{{{n}^{2}}}{{\sin }^{2}}\theta \}}^{1/2}}+\pi \]
B. \[\dfrac{4\pi d}{\lambda }{{\{1-\dfrac{1}{{{n}^{2}}}{{\sin }^{2}}\theta \}}^{1/2}}\]
C. \[\dfrac{4\pi d}{\lambda }{{\{1-\dfrac{1}{{{n}^{2}}}{{\sin }^{2}}\theta \}}^{1/2}}-\pi \]
D. \[\dfrac{4\pi d}{\lambda }{{\{1+\dfrac{1}{{{n}^{2}}}{{\sin }^{2}}\theta \}}^{1/2}}\]

Answer 1

Hint: When a light ray travelling from one medium to another undergoes refraction of light then there is change in the path of the light and that can be explained using Snell’s law. When the light ray travels from a rarer medium to a denser medium it moves towards the normal while in the opposite scenario, it moves away from the normal.

Complete step by step solution:

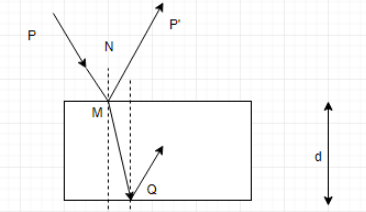
We have refraction at points M and Q. Let the angle of incidence at point M be \[\theta \] and the angle of refraction be r. Also, let at point Q let the angle of incidence, on account of alternate interior angles, the angle of incidence be r and the angle of reflection be r’.
Now time taken by the light to travel along MQ is \[t=\dfrac{MQ}{c}\], since the speed of light is c in the vacuum and let v be the speed in the glass. Snell’s law= \[n=\dfrac{c}{v}\]
Using trigonometric ratios and using the relation, \[n=\dfrac{c}{v}\]

\[t=\dfrac{d/\cos r}{c/n}\]--(1)
Again from Snell’s law: \[n=\dfrac{\sin \theta }{\sin r}\]
$\Rightarrow \sin r=\dfrac{\sin \theta }{n} \\
\Rightarrow \cos r=\sqrt{1-{{\sin }^{2}}r} \\$
\[\Rightarrow \cos r=\sqrt{1-\dfrac{{{\sin }^{2}}\theta }{{{n}^{2}}}}\]--(2)
Phase difference is given by the relation: \[\Delta \phi =\dfrac{2\pi }{T}\times t\]
$\Rightarrow \Delta \phi =\dfrac{2\pi }{T}\times \dfrac{nd}{c\times \cos r} \\
\Rightarrow \Delta \phi =\dfrac{2\pi nd}{\lambda }{{\{1-\dfrac{{{\sin }^{2}}\theta }{{{n}^{2}}}\}}^{-1/2}} \\$
Now net phase difference will be \[\Delta \phi +\pi \]
\[\therefore \Delta \phi =\dfrac{2\pi nd}{\lambda }{{\{1-\dfrac{{{\sin }^{2}}\theta }{{{n}^{2}}}\}}^{-1/2}}+\pi \]

So, the correct option is A.

Note: If a ray is incident obliquely that is perpendicular to the glass surface then it moves into the second medium undeviated. Here ray is totally internally reflected it is a special case in which light travelling from a denser medium to rarer medium.While using snell's law the refractive index is given by the ratio of refractive of the refractive index of the second medium to the refractive index of first medium. Be careful while the angles of reflection, refraction and of incidence are always made with the normal.