Question

Consider a pyramid OPQRS located in the first octant $\left( {x \geqslant 0,y \geqslant 0,z \geqslant 0} \right)$ with O as origin, and OP and OR along the x-axis and the y-axis, respectively. The base OPQR of the pyramid is a square with $OP = 3.$ The point S is directly above the midpoint T of diagonal OQ such that $TS = 3.$ Which of the following options is correct?
(A) The acute angle between OQ and OS is $\dfrac{\pi }{3}$
(B) The equation of the plane containing the triangle OQS is $x - y = 0$
(C) The length of the perpendicular from P to the plane containing the triangle OQS is $\dfrac{3}{{\sqrt 2 }}$
(D) The perpendicular distance from O to the straight line containing RS is $\sqrt {\dfrac{{15}}{2}} $

Answer 1

Hint:Analyse all the given information in the question using a rough diagram. After completing the diagram, start with finding the corner points of the pyramid OPQRS. Now use this information to check for each of the options one by one. For (A) use scalar product to find the angle, i.e. $\overrightarrow A \cdot \overrightarrow B = \left| A \right|\left| B \right| \times \cos \theta $. For (B) use a vector or cross product to find the normal vector. Now check the results and find the correct option.


Complete step-by-step answer:

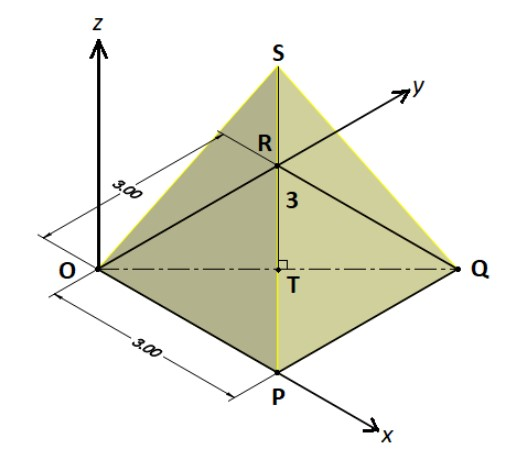
Before starting with the solution, let’s start with analyzing the given information using a diagram. Here we have a pyramid OPQRS, having its base on the x-y plane. Its base is a square of side length $3units$. It is also given that point P lies on the x-axis and point R lies on y-axis. Point T is the midpoint of the diagonal OQ of the base. Point S lies exactly above T with $TS = 3units$ . So, with all this information we can draw a diagram as shown in the figure.
Let’s first start with finding the coordinates of points O, P, Q, R and S.
Point O is the origin, i.e. $O\left( {0,0,0} \right)$
Point P lies on the x-axis with $OP = 3$. So it has its y and z-axis coordinates as zero, therefore the coordinates will be $\left( {3,0,0} \right)$
Point R lies on the y-axis with $OR = 3$. So it has its x and z-axis coordinates as zero, therefore the coordinates will be $\left( {0,3,0} \right)$
Point Q lies in the x-y plane with distance from both the axis as $3units$. So, it will have z-axis coordinate as zero, therefore the coordinates will be $\left( {3,3,0} \right)$
Since we know that the point T lies on midpoint of diagonal OQ, the coordinates of point will be $\left( {\dfrac{3}{2},\dfrac{3}{2},0} \right)$
Point S lies just above the point T at a distance of $3units$. Therefore, the coordinates of point S will be $\left( {\dfrac{3}{2},\dfrac{3}{2},3} \right)$
Since O is the origin, then vectors for OS and OQ can be written as: $\overrightarrow {OS} = \dfrac{3}{2}\hat i + \dfrac{3}{2}\hat j + 3\hat k$ and $\overrightarrow {OQ} = 3\hat i + 3\hat j$
The scalar product of two vectors $\overrightarrow A {\text{ and }}\overrightarrow B $ , with an angle $\theta $ between these vectors, can be defined as:$\overrightarrow A \cdot \overrightarrow B = \left| A \right|\left| B \right| \times \cos \theta $ , where $\left| {\overrightarrow A } \right|$ represents the magnitude of the vector $\overrightarrow A $ .
Let’s use to find the scalar product of $\overrightarrow {OS} {\text{ and }}\overrightarrow {OQ} $
$ \Rightarrow \overrightarrow {OS} \cdot \overrightarrow {OQ} = \left( {\dfrac{3}{2}\hat i + \dfrac{3}{2}\hat j + 3\hat k} \right) \cdot \left( {3\hat i + 3\hat j} \right) = \sqrt {{{\left( {\dfrac{3}{2}} \right)}^2} + {{\left( {\dfrac{3}{2}} \right)}^2} + {{\left( 3 \right)}^2}} \times \sqrt {{{\left( 3 \right)}^2} + {{\left( 3 \right)}^2}} \times \cos \theta $
Now we can solve the dot product in this equation for the value of $\theta $
$ \Rightarrow \left( {\dfrac{3}{2} \times 3 + \dfrac{3}{2} \times 3 + 0} \right) = \sqrt {\dfrac{9}{4} + \dfrac{9}{4} + 9} \times \sqrt {9 + 9} \times \cos \theta $
Solving it further, we get:
$ \Rightarrow \left( {\dfrac{9}{2} + \dfrac{9}{2}} \right) = \dfrac{{3\sqrt 3 }}{{\sqrt 2 }} \times 3\sqrt 2 \times \cos \theta $
$ \Rightarrow 9 = 9\sqrt 3 \times \cos \theta $
Therefore, we get: $\cos \theta = \dfrac{1}{{\sqrt 3 }} \Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right)$
Therefore Option A is incorrect.

Let's check for Option B
Now let’s find the plane that contains triangle OQS
For finding normal vector to this plane we need to find the cross product of the vector $\overrightarrow {OQ} {\text{ and }}\overrightarrow {OS} $
\[ \Rightarrow \overrightarrow n = \overrightarrow {OQ} \times \overrightarrow {OS} = \left( {3\widehat i + 3\widehat j} \right) \times \left( {\dfrac{3}{2}\widehat i + \dfrac{3}{2}\widehat j + 3\widehat k} \right) = \left| {\begin{array}{*{20}{c}}
  {\widehat i}&{\widehat j}&{\widehat k} \\
  3&3&0 \\
  {\dfrac{3}{2}}&{\dfrac{3}{2}}&3
\end{array}} \right| = \widehat i\left( {9 - 0} \right) - \widehat j\left( {9 - 0} \right) + \widehat k\left( {\dfrac{9}{2} - \dfrac{9}{2}} \right) = 9\widehat i - 9\widehat j\] Now let us assume a position vector $\overrightarrow r = x\widehat i + y\widehat j + z\widehat k$ that lies on the required plane. Therefore, we can say: $ \Rightarrow \overrightarrow r \cdot \overrightarrow n = 0$ . This will be our required equation for the plane.
Substituting the value of both vectors and finding dot product:
$ \Rightarrow \overrightarrow r \cdot \overrightarrow n = 0 \Rightarrow \left( {x\widehat i + y\widehat j + z\widehat k} \right) \cdot \left( {9\widehat i - 9\widehat j} \right) = 0 \Rightarrow 9x - 9y = 0 \Rightarrow 9\left( {x - y} \right) = 0$
Therefore, we get the equation of the plane containing triangle OQS as $x - y = 0$

Now, let’s move on to option (C)
For finding the length of the perpendicular from P to the plane containing the triangle OQS, we just need to find the shortest distance from the point $P\left( {3,0,0} \right)$ to the plane $x - y = 0$
Since we know that the shortest distance between a point $\left( {{x_1},{y_1},{z_1}} \right)$ and the plane $ax + by + cz + d = 0$ can be given by $\left| {\dfrac{{a{x_1} + b{y_1} + c{z_1} + d}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}} \right|$
By using that, the distance required\[ = \left| {\dfrac{{3 - 0}}{{\sqrt {{1^2} + {1^2}} }}} \right| = \dfrac{3}{{\sqrt 2 }}\]

Considering the option (D)
For finding the perpendicular distance from O to the straight line containing RS, we need to find the perpendicular distance from origin, i.e. $\left( {0,0,0} \right)$ to the straight line that passes through point $R\left( {0,3,0} \right)$ and $S\left( {\dfrac{3}{2},\dfrac{3}{2},3} \right)$
The direction vector for $\overrightarrow {RS} $ can be written as: $\overrightarrow {RS} = \widehat i\left( {\dfrac{3}{2} - 0} \right) + \widehat j\left( {\dfrac{3}{2} - 3} \right) + \widehat k\left( {3 - 0} \right) = \dfrac{3}{2}\widehat i - \dfrac{3}{2}\widehat j + 3\widehat k$
As we know that, the equation of a line passing through the point $A\left( {{x_1},{y_1},{z_1}} \right)$ and with direction ratios as $\left\langle {a,b,c} \right\rangle $ can be written as: $\dfrac{{x - {x_1}}}{a} = \dfrac{{y - {y_1}}}{b} = \dfrac{{z - {z_1}}}{c}$
By using that, we get the equation of line as: $\dfrac{{x - 0}}{{\dfrac{3}{2}}} = \dfrac{{y - 3}}{{\dfrac{{ - 3}}{2}}} = \dfrac{{z - 0}}{3}$
This can be further simplified by multiplying and divide with $\dfrac{3}{2}$ as:
\[ \Rightarrow \dfrac{3}{2} \times \dfrac{{x - 0}}{{\dfrac{3}{2}}} = \dfrac{3}{2} \times \dfrac{{y - 3}}{{\dfrac{{ - 3}}{2}}} = \dfrac{3}{2} \times \dfrac{{z - 0}}{3} \Rightarrow \dfrac{{x - 0}}{1} = \dfrac{{y - 3}}{{ - 1}} = \dfrac{{z - 0}}{2} = \lambda………………….(i)\]
Now let’s assume a point $A\left( {h,k,l} \right)$ that lies on line RS and line OA is perpendicular. So now we just have to find distance OA.
Since OA is perpendicular to line RS, this implies that the dot product of the direction vector of the line (i) and OA will be zero
$ \Rightarrow \overrightarrow {OA} \cdot \left( {\widehat i - \widehat j + 2\widehat k} \right) = 0 \Rightarrow \left( {h\widehat i + k\widehat j + l\widehat k} \right) \cdot \left( {\widehat i - \widehat j + 2\widehat k} \right) = 0 \Rightarrow h - k + 2l = 0 ………...(ii)$
Also, this point A satisfies the line (i)
$ \Rightarrow \dfrac{h}{1} = \dfrac{{k - 3}}{{ - 1}} = \dfrac{l}{2} = \lambda $
Therefore, we can write: $h = \lambda ,l = 2\lambda {\text{ and }}k = - \lambda + 3……..(iii)$
Now, we can substitute the values found in (iii) to the equation (ii)
$ \Rightarrow h - k + 2l = \lambda + \lambda - 3 + 4\lambda = 6\lambda - 3 = 0 \Rightarrow \lambda = \dfrac{1}{2}$
So, using the value of $\lambda $ in (iii), we get:
$ \Rightarrow h = \dfrac{1}{2},l = 1{\text{ and }}k = \dfrac{{ - 1}}{2} + 3 = \dfrac{5}{2}$
Now, we have point $O\left( {0,0,0} \right)$ and point $A\left( {\dfrac{1}{2},\dfrac{5}{2},1} \right)$ and we have to find the distance of point A from the origin.
This can be given by $\left| {\overrightarrow {OA} } \right| = \sqrt {{h^2} + {k^2} + {l^2}} = \sqrt {{{\left( {\dfrac{1}{2}} \right)}^2} + {{\left( {\dfrac{5}{2}} \right)}^2} + {1^2}} = \sqrt {\dfrac{{1 + 25 + 4}}{4}} = \sqrt {\dfrac{{30}}{4}} = \sqrt {\dfrac{{15}}{2}} $
So, we get the perpendicular distance from O to the straight line containing RS as $\sqrt {\dfrac{{15}}{2}} $

So, the correct answer is “Option B , C and D”.

Note:In questions like this, where you have some information in the question and then multiple options answers, you should always check for each option one by one. Always start with drawing a rough diagram which will enhance your understanding and visualisation. Notice that we used symbol$'\left| {\overrightarrow A } \right|'$ , which simply represents the magnitude of the vector A and it can be found by taking the square root of the sum of squares of three coordinates. Do not confuse the use of dot or scalar product and cross or the vector product of vectors. Both can be applied on two vectors but dot product will give a scalar quantity whereas a cross-product will give a vector in the direction perpendicular to the two vectors.