Question

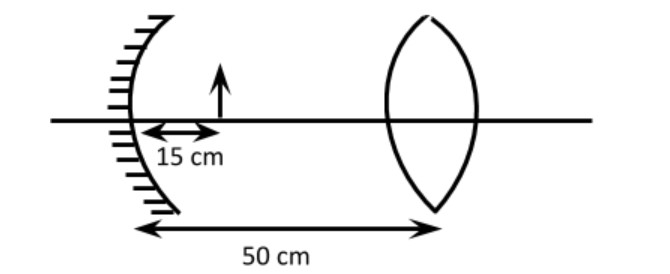
Consider a concave mirror and a convex lens (refractive index $ = 1.5$) of focal length $10{\text{cm}}$ each, separated by a distance of \[50{\text{cm}}\] in air (refractive index \[ = 1\]) as shown in the figure. An object is placed at a distance of \[15{\text{cm}}\] from the mirror. Its erect image formed by this combination has magnification \[{{\text{M}}_{\text{1}}}\]. When the set-up is kept in a medium of refractive index \[\dfrac{7}{6}\], the magnification becomes \[{{\text{M}}_{\text{2}}}\]. The magnitude \[\left| {\dfrac{{{M_2}}}{{{M_1}}}} \right|\] is

Answer 1

Hint: The first image from reflection by a spherical concave mirror can be found from mirror formula.

Formula used:
$
  \dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f} \\
  \dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f} \\
  m = \dfrac{v}{u} \\
  M = {m_1} \times {m_2} \\
 $

Complete step by step solution:
Given data,
For concave mirror
$u = - 15cm,{\text{ f}} = - 10cm$
As we know,
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
$
  \therefore \dfrac{1}{v} + \dfrac{1}{{ - 15}} = \dfrac{1}{{ - 10}} \\
   \Rightarrow \dfrac{1}{v} = \dfrac{{ - 1}}{{10}} + \dfrac{1}{{15}} = \dfrac{{10 - 15}}{{150}} \\
   \Rightarrow v = - 30cm \\
 $
Dividing (1) by (2)
$
  \dfrac{{{f_{liquid}}}}{{{f_{air}}}} = \dfrac{{\dfrac{1}{2}}}{{\dfrac{3}{2} \times \dfrac{6}{7} - 1}} \\
   = \dfrac{7}{4} \\
 $
$
  {f_{liquid}} = \dfrac{7}{4} \times 10 \\
   = \dfrac{{70}}{4}cm \\
 $
The first image will act as an object for lens and its position can be found using lens formula,
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$

Given:
$
  u = - 20cm, {\text{ f}} = \dfrac{{70}}{4}cm \\
    \\
 $
$\therefore \dfrac{1}{v} - \dfrac{1}{{ - 20}} = \dfrac{1}{{\dfrac{{70}}{4}}}$
$ \Rightarrow \dfrac{1}{v} \times \dfrac{4}{{70}} = \dfrac{{80 - 70}}{{1400}}$
$ \Rightarrow v = 140cm$
Magnification is given by $m' = \dfrac{v}{u} = \dfrac{{140}}{{ - 20}} = - 7$
Total magnification ${m_2} = - 2 \times - 7 = 14$

Hence, $\left| {\dfrac{{{m_2}}}{{{m_1}}}} \right| = \dfrac{{14}}{2} = 7$

Note: Focal length of lens depends on the medium in which the whole experiment is done. Students must be careful while taking sign convention.