Question

Complete the refracted ray in the following ray diagram.

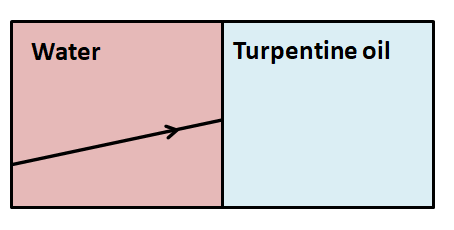
Answer 1

Hint: To solve this question, we need to compare the refractive indices of the water and the turpentine oil. Light is bent more in a medium whose refractive index is more. The bending of the light between two mediums is with reference to the normal to the interface separating the two mediums.

Formula used: The formula used to solve this question is given by
\[{\mu _1}\sin {{{\theta }}_1} = {\mu _2}\sin {{{\theta }}_2}\], here ${\mu _1}$ and ${\mu _2}$ are the refractive indices of the first and the second mediums respectively. And ${{{\theta }}_1}$ and ${{{\theta }}_2}$ are the made by the ray of light in the respective mediums, with the normal to the interface separating the two mediums.

Complete step by step answer:
Let the refractive indices of water be ${\mu _w}$ and that of the turpentine oil be ${\mu _t}$. Also let ${{{\theta }}_w}$ and ${{{\theta }}_t}$ be the angles made by the ray with the normal to the interface in the respective mediums.
We know from the Snell’s law that
${\mu _w}{{sin}}\left( {{{{\theta }}_w}} \right) = {\mu _t}{\text{sin}}\left( {{{{\theta }}_t}} \right)$
\[ \Rightarrow \sin {{{\theta }}_t} = \dfrac{{{\mu _w}}}{{{\mu _t}}}\sin {{{\theta }}_w}\]_____(1)
Now, we know that the refractive index of water is equal to $1.33$ and that of the turpentine oil is about $1.46$, so that we can write
${\mu _w} = 1.33$_______(2)
${\mu _t} = 1.46$__________(3)
Substituting (2) and (3) un (1) we gey
\[\sin {{{\theta }}_t} = \dfrac{{1.33}}{{1.46}}\sin {{{\theta }}_w}\]
$ \Rightarrow \sin {{{\theta }}_t} = 0.91\sin {{{\theta }}_w}$
So we can say that
\[\sin {{{\theta }}_t} < \sin {{{\theta }}_w}\]
Since both the angles ${{{\theta }}_w}$ and ${{{\theta }}_t}$ are measured with the normal, so they lie in the first quadrant. So we can say that
\[{{{\theta }}_t} < {{{\theta }}_w}\]
Therefore the angle made by the light ray in the turpentine oil is less than that in the water. So the refracted ray must bend towards the normal. Hence, we complete the refracted ray as shown in the below diagram.

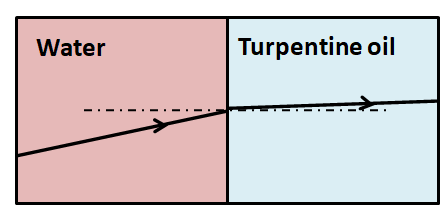
Note: In case we do not remember the exact values for the refractive indices of the two mediums given in this question, then also we can attempt this question just by using common sense. We just need to compare the angles made in the two mediums. So we can use the fact that the turpentine oil is denser than water so it must have a greater refractive index.