Question

Classify the following angle as acute, obtuse, straight, right, zero, and complete angle. ${{30}^{\circ }}$.

Answer 1

Hint: We first define the given options of acute, obtuse, straight, right, zero and complete angle. We take examples and conditions to understand the types of angles better. In the end, we place the given angle in its appropriate group.

Complete step-by-step solution:
We first define different types of angles like acute, obtuse, straight, right, zero, and complete angles.
According to the value of the angle, it can be broken into three parts.
The acute angles are those angles, which are between 0 and 90. So, if x is an acute angle then ${{0}^{\circ }}< x< {{90}^{\circ }}$.
The obtuse angles are those angles, which are between 90 and 180. So, if y is an obtuse angle then ${{90}^{\circ }}< y< {{180}^{\circ }}$.
The right angle is the angle, which has a value of 90. So, if p is a right angle then $p={{90}^{\circ }}$.
The zero angles are the angle, which has the value of 0. So, if m is a zero angle then $m={{0}^{\circ }}$.
The complete angle is the angle which has the value of 360. So, if t is a complete angle then $t={{360}^{\circ }}=2\pi $.
So, ${{30}^{\circ }}$ is an acute angle as \[{{0}^{\circ }}< {{30}^{\circ }}<{{90}^{\circ }}\]. In the following image $\angle ABC={{30}^{\circ }}$.

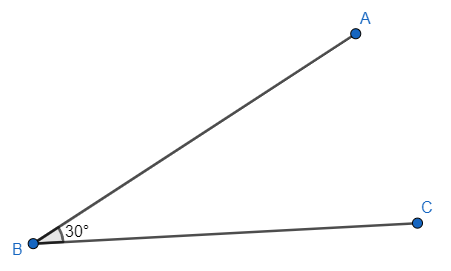
Note: We need to remember that the angles with measurement greater than 180 and less than 360 are called the reflex angle. So, if x is a reflex angle then ${{180}^{\circ }}< x< {{360}^{\circ }}$. Also, we can use the trick of using starting letters of acute and obtuse to remember their characteristics. The word ‘acute’ starts with a and the word ‘obtuse’ starts with o. As a comes first that’s why acute angle represents ${{0}^{\circ }}< x< {{90}^{\circ }}$ and obtuse angle represents ${{90}^{\circ }}< y< {{180}^{\circ }}$.