Question

Choose the correct statement on the basis of the paragraph.
(This question has multiple correct options)
A. dot product means multiplying the magnitude of A to the projection of B on A.
B. dot product means multiplying two vectors along X axis.
C. dot product means multiplying a vector by the perpendicular projection of the other vector on the first vector.
D. dot product makes the result a scalar.

Answer 1

Hint:The Dot product of two vectors is given by, $\overrightarrow A \cdot \overrightarrow B = ab\cos \theta $ .
Here, a, and b are the magnitudes of vector A and vector B respectively and $\theta $ is the angle between them.

Complete step-by-step solution:

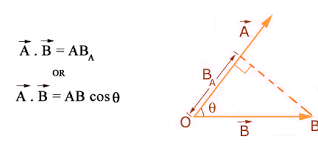
In the figure above the two vectors A and B make an angle $\theta $ . Here the magnitude of vector A is A and the magnitude of vector B is B.
Now, for the above figure we define Dot product as, ‘the product of magnitude of vector A and the projection of vector B on vector A.’
Now,
The magnitude of vector A ($\overrightarrow A $ ) = A ----------- (given)
The magnitude of vector B ($\overrightarrow B $ ) = B ----------- (given)
So, the projection of $\overrightarrow B $ on $\overrightarrow A $ =$B\cos \theta $ --------- (by definition of horizontal projection)
Thus by definition of Dot product of vectors,
Dot product of $\overrightarrow A $ and $\overrightarrow B $ = $\overrightarrow A \cdot \overrightarrow B = AB\cos \theta $ -------- (equation: 1)
In equation: 1, $A$ is the magnitude of $\overrightarrow A $ , and $B\cos \theta $ is the projection of $\overrightarrow B $ on $\overrightarrow A $ .
Thus, the dot product is multiplying the magnitude of A to the projection of B on A.
Hence, option A is correct.
Dot product tells you what amount of one vector goes in the direction of another vector.
For instance in the above figure $\overrightarrow B $ is not along $\overrightarrow A $ but at an angle $\theta $ with the same.
So, the dot product $\overrightarrow A \cdot \overrightarrow B = AB\cos \theta $ tells us what amount of $\overrightarrow B $ is along (in the direction) of $\overrightarrow A $ .
Hence, option B and option C are incorrect.
Now, as we all know quantities are divided into two categories:
1. Vectors (having magnitude and direction).
2. Scalars (having only magnitude)
In equation: 1 you can see that all the terms are scalars, since all are just magnitude, the dot product is actually a product of scalars.
Also, a product of two scalar quantities is a scalar quantity.
Hence, dot product makes the result a scalar.
So, option D is also correct.
Thus, the answers to this question are option A and option D.

Note:-
->Dot product of perpendicular vectors is zero, as the angle between them is 90 degrees the cosine of 90 is zero.
->Dot product’s definition tells it is all about horizontal projections so do not consider perpendicular projections while calculating dot products.
It is always helpful to draw a rough diagram to get a better understanding of the problem.