Question

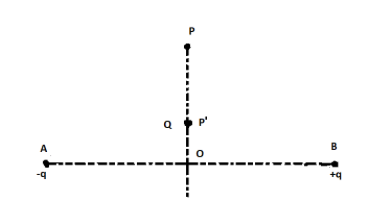
Charge $ - q$ and $ + q$ located at A and B, respectively, constitute an electric dipole. Distance AB = $2a$, O is the mid point of the dipole and OP is perpendicular to AB. A charge Q is placed at P where OP = $y$ and $y > > 2a$. The charge $Q$ experiences and electrostatic force $F$. If $Q$ is now moved along the equatorial line to ${P'}$ such that $O{P'} = (\dfrac{y}{3})$ the force on $Q$ will be close to $L$ : $(\dfrac{y}{3} > > 2a)$

A) $\dfrac{F}{3}$
B) $3F$
C) $9F$
D) $27F$

Answer 1

Hint:In order to solve this question one should be aware of the concept of electrostatic forces and how the net electrostatic force is calculated. Here, in this question, charge $Q$ experiences force which is the resultant of both $ - q$ and $ + q$. Also, remember that $y > > 2a$. So, we can neglect $a$ when higher powers are taken.

Complete step by step answer:
Here the charge $Q$ will experience an electrostatic force due to both $ - q$ and $ + q$, the force $F$ is the resultant force applied by both $ - q$ and $ + q$ .
The electrostatic force between any two charges is given by
$F = \dfrac{{{q_1}{q_2}}}{{{r^2}}}$
Here ${q_1}$ and ${q_2}$ are the two charges.
$r$ is the distance between the two charges.
Let the force applied by charge $ - q$ on $Q$ when it is placed at point P be ${F_A}$ so ${F_A}$ would be given by
${F_A} = \dfrac{{qQ}}{{{{(\sqrt {{y^2} + {a^2}} )}^2}}}$
As, $y > > 2a$
So, ${F_A} = \dfrac{{qQ}}{{{y^2}}}$
Similarly, Let the force applied by charge $ + q$ on $Q$ when it is placed at point P be ${F_B}$ so ${F_B}$ would be given by ${F_B} = \dfrac{{qQ}}{{{y^2}}}$
For the net force we have to calculate the resultant force on $Q$
Here, the components of $\sin \theta $ would get cancelled and only $\cos \theta $ component would be added.
So, $F = {F_A}\cos \theta + {F_B}\cos \theta $
Here, $\cos \theta = \dfrac{a}{{\sqrt {{y^2} + {a^2}} }}$
As, $y > > 2a$

 $\cos \theta = \dfrac{a}{y}$
So, the net force would become, $F = ({F_A} + {F_B}) \times \dfrac{a}{y}$
$F = (\dfrac{{2qQ}}{{{y^2}}}) \times \dfrac{a}{y}$
On simplifying we get,
$F = \dfrac{{2aqQ}}{{{y^3}}}$ ………. Equation 1
Now when the charge $Q$ is put at ${P'}$
We have the distance between the charges as $\dfrac{y}{3}$
So, putting $y$ as $\dfrac{y}{3}$ in the equation 1 we get,
${F'} = 27 \times (\dfrac{{2aqQ}}{{{y^3}}})$
Hence, ${F'} = 27F$

So, option D is the correct answer.

Note:Always remember that like charges repel each other and unlike or opposite charges attract each other. If two charges are at rest then the force between them is known as electrostatic force. This force between charges increases when the magnitude of the charges increases and also when the distance between the charges decreases.