Question

Charge 2Q and –Q are placed as shown in figure. At what point electric field intensity will be zero?

A. Between –Q and 2Q
B. On the left of –Q
C. On the right of 2Q
D. On the perpendicular bisector of line joining the charges

Answer 1

Hint: To determine the point where electric field is zero, we first obtain expression for net field due to both the charges and equate it to zero. The zeroes of the equation gives us the point where the net electric field is zero.

Formula used: Electric field intensity due to a single charge, $\vec{E}=\dfrac{q}{4\pi {{\epsilon }_{0}}{{r}^{2}}}\hat{r}$

Complete step by step answer:
 Electric field intensity is defined as electrostatic force experienced by a unit positive charge when placed in an electric field. Electric field intensity at a point due to a single charge in free space is given by
$\vec{E}=\dfrac{q}{4\pi {{\epsilon }_{0}}{{r}^{2}}}\hat{r}$
Where $q$ is the magnitude of charge, $\epsilon_0$ is permittivity of free space and $r$ is the distance of that point from the position of electric charge.
In this question two charges –Q and 2Q are placed along the x-axis at some distance, say $r$. Let us assume that charge –Q is placed at origin. Due to symmetry, the point will also lie on the x-axis. Let’s assume the point is at distance $x$ from origin.

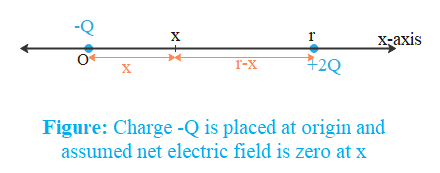
Electric field intensity due to charge –Q at $x$ will be:
${{\vec{E}}_{1}}=\dfrac{-Q}{4\pi {{\epsilon }_{0}}}\dfrac{1}{{{x}^{2}}}$
Negative sign shows that electric field is towards the charge -Q
Electric field intensity due to charge +2Q at $x$ will be:
${{\vec{E}}_{2}}=\dfrac{+2Q}{4\pi {{\epsilon }_{0}}}\dfrac{1}{{{(r-x)}^{2}}}$
Positive sign shows that electric field is away from the charge +2Q
Since charge +2Q is placed at ($r$), the distance of ($x$) from respective coordinate is $\left| r-x \right|$
Since, the net electric field due to both the charges is zero at point $x$. Therefore,
${{\vec{E}}_{x,y}}={{\vec{E}}_{1}}+{{\vec{E}}_{2}}=0$
$\dfrac{-Q}{4\pi {{\epsilon }_{0}}}\dfrac{1}{{{x}^{2}}}+\dfrac{2Q}{4\pi {{\epsilon }_{0}}}\dfrac{1}{{{(r-x)}^{2}}}=0$
 $\dfrac{Q}{4\pi {{\epsilon }_{0}}}\left( \dfrac{2}{{{(r-x)}^{2}}}-\dfrac{1}{{{x}^{2}}} \right)=0$
$\Rightarrow \dfrac{2}{{{(r-x)}^{2}}}-\dfrac{1}{{{x}^{2}}}=0$
$\Rightarrow {{x}^{2}}+2xr-{{r}^{2}}=0$
We can find the zeroes of this equation to find the position where the electric field due to charge configuration is zero.
Since for a quadratic equation, ${{x}_{0}}=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$ where ${{x}_{0}}$is the zero of equation $a{{x}_{0}}^{2}+b{{x}_{0}}+c=0$
On comparing both the equations we get,
$a=1,\text{ }b=2r\text{ and }c=-{{r}^{2}}$
We substitute these values and get,
$x=(-1\pm \sqrt{2})r$
From these points one lies to the left of charge +-Q and another one lies between both charges. But if we place a small positive test charge between two charges, it would always be "pushed" harder to the left by the bigger charge and it would be "pulled" to the left by the smaller charge, so it cannot be there. If we place a small positive charge to the left it will be pulled to the right by the nearby negative charge and pushed to the left by a more distant, but larger positive charge, so the balance point must be somewhere here.
Hence, we conclude that point where electric field intensity will be zero is $x=(-1-\sqrt{2})r$

So, the correct answer is “Option B”.

Note: Sometimes students might get confused and think that the electric field will be zero at two points. The electric field will be zero at a point nearer to a smaller charge when the system consists of two opposite and unequal charges.
The electric field due to a dipole is never zero at any point around the dipole.