Question

What is the center and radius of the circle ${x^2} + {y^2} - 2x + 4y - 4 = 0$?

Answer 1

Hint: To find the center and radius of the circle ${x^2} + {y^2} - 2x + 4y - 4 = 0$, first of all convert the given equation into standard form of circle equation by following the steps explained below. After the conversion is done, you have to compare the obtained equation with the standard equation of the circle.
Standard equation of circle with center $\left( {a,b} \right)$ and radius r is
$ \Rightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$

Complete step-by-step answer:
In this question, we are given an equation of the circle and we have to find its radius and center.
Now, the standard equation of a circle with center $\left( {a,b} \right)$ and radius r is given by
$ \Rightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$- - - - - - (1)
Using this equation, you can find the center and radius of the circle easily.
But, usually the circle equations are given in form $a{x^2} + b{y^2} + cx + dy + e = 0$. So, to find the center and the radius of the circle, we have to complete the square and convert the given equation to the standard equation of the circle.
Given equation: ${x^2} + {y^2} - 2x + 4y - 4 = 0$- - - - - - - - - (2)
So, we have to convert this equation to the standard form of the circle equation.
Steps of conversion:
Step 1:
Take the constant term to the other side of equal to. Therefore, equation (2) becomes,
$ \Rightarrow {x^2} + {y^2} - 2x + 4y = 4$- - - - - - - - (3)
Step 2:
Group the $x$ terms together and the $y$ terms together. Therefore, equation (3) becomes
$ \Rightarrow \left( {{x^2} - 2x} \right) + \left( {{y^2} + 4y} \right) = 4$- - - - - - - (4)
Step 3:
Make the coefficient of square terms 1 by dividing the term. In this case, it is already 1.
Step 4:
Take the coefficient of $x$ and then multiply it by $\dfrac{1}{2}$ and then square it. Now, add the answer to both sides of the equation.
So, here the coefficient of $x$ is $ - 2$.
$ \Rightarrow - 2 \times \dfrac{1}{2} = {\left( { - 1} \right)^2} = 1$
So, we will add 1 on both sides of the equation.
Do the same process for y as well.
$ \Rightarrow 4 \times \dfrac{1}{2} = {\left( 2 \right)^2} = 4$
So, we will also add 4 to the both sides of the equation.
Therefore, equation (4) will become
$
   \Rightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} + 4y + 4} \right) = 4 + 1 + 4 \\
   \Rightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} + 4y + 4} \right) = 9 \\
 $
Now, $\left( {{x^2} - 2x + 1} \right) = {\left( {x - 1} \right)^2}$ and $\left( {{y^2} + 4y + 4} \right) = {\left( {y + 2} \right)^2}$ and $9 = {3^2}$.
Therefore, the above equation will become
$ \Rightarrow {\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = {3^2}$- - - - - - - (5)
And now we can compare equations (1) and (5) to get the center and the radius of the circle.
Therefore, $a = 1,b = - 2,r = 3$
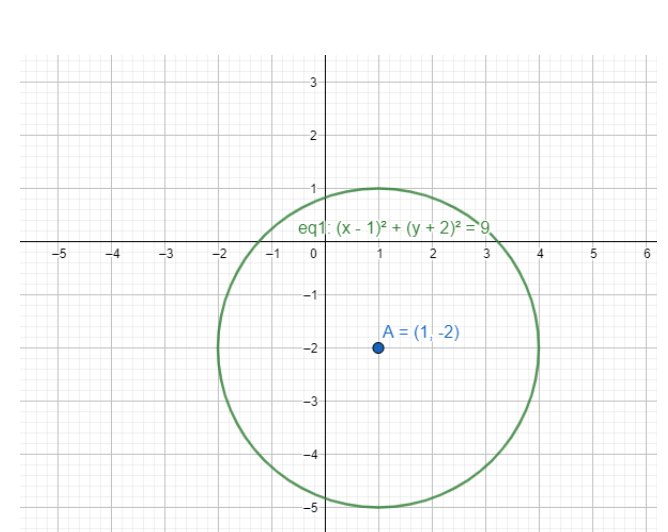
Therefore, the center of the circle is$\left( {1, - 2} \right)$ and the radius is 3.
Let us represent this circle on a graph.

Note: We can also obtain the center and radius of the circle using the general equation of circle. The general equation of circle is
$ \Rightarrow {x^2} + {y^2} + 2gx + 2fy + c = 0$
$ \Rightarrow Center = \left( { - g, - f} \right)$
$ \Rightarrow Radius = \sqrt {{g^2} + {f^2} - c} $
So, here our equation is ${x^2} + {y^2} - 2x + 4y - 4 = 0$. Therefore,
$g = - 1$ and $f = 2$ and $c = - 4$
Therefore,
$ \Rightarrow Center = \left( { - g, - f} \right) = \left( { - 1,2} \right)$
$ \Rightarrow Radius = \sqrt {{g^2} + {f^2} - c} = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( 2 \right)}^2} - \left( { - 4} \right)} = \sqrt 9 = 3$