Question

Car A and car B start moving simultaneously in the same direction along the line joining them. Car A is with constant acceleration a = $ 4m{{s}^{-2}} $ . While carB moves with constant velocity v = 1m/s. At t = 0 car A is 10m behind car B. find the time when car A overtakes car B.
(A) 2s
(B) $ 2.5 $ s
(C) 1s
(D) $ 1.5 $ s

Answer 1

Hint: Find the relative velocity and relative acceleration and then using those values in Newton's second equation of motion we can get the time taken by car A to overtake car B.
Relative velocity is defined as the velocity of an object B in the rest frame of another object A.
Relative acceleration is the comparison of the acceleration of two bodies.
Newton’s second equation of motion is given as:
 $\Rightarrow s=ut+\dfrac{1}{2}a{{t}^{2}} $.

Complete step by step solution

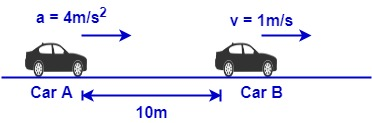
Here,
 $\Rightarrow {{u}_{A}}=0 $
 $\Rightarrow {{u}_{B}}=1m/s $
 $\Rightarrow {{u}_{AB}}={{u}_{A}}-{{u}_{B}} $
 $\Rightarrow {{u}_{AB}}=0-1 $
 $\Rightarrow {{u}_{AB}}=-1m/s $
Also,
 $\Rightarrow {{a}_{A}}=4m/{{s}^{2}} $
 $\Rightarrow {{a}_{B}}=0 $
 $\Rightarrow {a_{AB}}={a_A}-{a_B} $
 $\Rightarrow {{a}_{AB}}=4-0 $
 $\Rightarrow {{a}_{AB}}=4m/{{s}^{2}} $
Now using Newton’s second equation of motion i.e.
 $\Rightarrow s=ut+\dfrac{1}{2}a{{t}^{2}} $
Here, s = 10m
And u, t and are the relative terms
So,
 $ \begin{align}
 &\Rightarrow 10=(-1)t+\dfrac{1}{2}(4){{t}^{2}} \\
 &\Rightarrow 10=-t+2{{t}^{2}} \\
 &\Rightarrow 2{{t}^{2}}-t-10=0 \\
\end{align} $
Solving the quadratic equation;
 $\Rightarrow t=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} $
Here, a = 2
b $ =-1 $
c $ =-10 $
We get;
 $\Rightarrow t=\dfrac{-(-1)\pm \sqrt{{{(-1)}^{2}}-4(2)(-10)}}{2(2)} $
 $\Rightarrow \dfrac{1\pm \sqrt{1-(-80)}}{4} $
 $\Rightarrow \dfrac{1\pm \sqrt{1+80}}{4} $
 $\Rightarrow \dfrac{1\pm \sqrt{81}}{4} $
 $\Rightarrow \dfrac{1\pm 9}{4} $
As a negative value of time is not possible so we will only take the positive values only.
 $\Rightarrow t=\dfrac{1+9}{4} $
 $\Rightarrow t=\dfrac{10}{4} $
 $\Rightarrow t=2.5s $
Therefore, option (B) is correct.

Note
In second equation of motion, remember to use the relative terms of velocity and acceleration as we are to calculate time of car A w.r.t. car B respectively. We have to remember some mathematical formulas like how to solve quadratic equations and some trigonometry. Using the concept of relative velocity and relative acceleration we can find out the speed of any object with respect to another object, that is we can compare two object's velocity and we can find out which object is moving with high speed and which is moving with low speed.