
Can someone please help me explain how to use the measures of right triangle to calculate the exact value of \[\sin {30^ \circ }\]? how can this information be used to determine the exact value of \[\sin {60^ \circ }\]?
Answer
536.1k+ views
Hint: We know that the right triangle has a side named hypotenuse and remaining two sides are base and height respectively. We also know the sin function is the ratio of opposite side to hypotenuses. This much data will help us to determine the values of sin function of \[\sin {30^ \circ }\] and \[\sin {60^ \circ }\].
Complete step by step solution:
First, we will draw a right triangle.
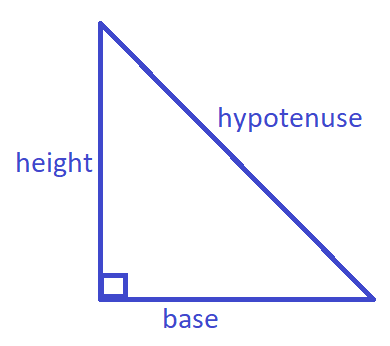
Now we have the diagram of the right triangle in front of us with one of the angles as the right angle and remaining two angles as either \[{60^ \circ }\]or \[{30^ \circ }\].
Now let’s draw the both cases and the ratios of the angles.
Thus in this way we found the ratio for both the angles. Now just putting the values of them we can get the answer.
Note: Note that we noted two cases above since the angle position is not mentioned. If it is given then use one of the situations that matches with one of the above. Also note that sin function is always the ratio of opposite side to hypotenuse but as the angle changes the value may change according to the angle so given.
Complete step by step solution:
First, we will draw a right triangle.

Now we have the diagram of the right triangle in front of us with one of the angles as the right angle and remaining two angles as either \[{60^ \circ }\]or \[{30^ \circ }\].
Now let’s draw the both cases and the ratios of the angles.
Case 1: 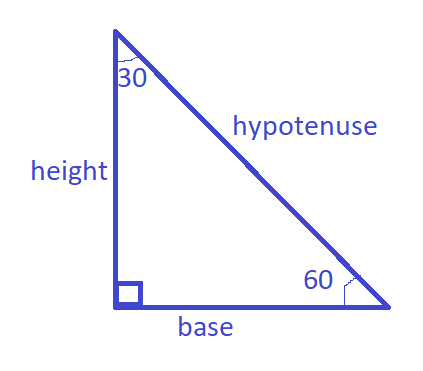
| Case 2: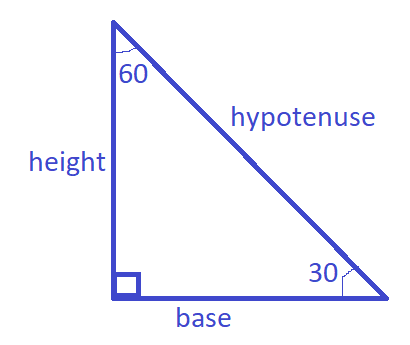
|
| \[\sin {30^ \circ } = \dfrac{{opp}}{{hypt}} = \dfrac{{base}}{{hypt}}\]\[\sin {60^ \circ } = \dfrac{{opp}}{{hypt}} = \dfrac{{height}}{{hypt}}\] | \[\sin {30^ \circ } = \dfrac{{opp}}{{hypt}} = \dfrac{{height}}{{hypt}}\]\[\sin {60^ \circ } = \dfrac{{opp}}{{hypt}} = \dfrac{{base}}{{hypt}}\] |
Thus in this way we found the ratio for both the angles. Now just putting the values of them we can get the answer.
Note: Note that we noted two cases above since the angle position is not mentioned. If it is given then use one of the situations that matches with one of the above. Also note that sin function is always the ratio of opposite side to hypotenuse but as the angle changes the value may change according to the angle so given.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Which cell organelles are present in white blood C class 11 biology CBSE

What is the molecular geometry of BrF4 A square planar class 11 chemistry CBSE

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

State the laws of reflection of light

Difference Between Prokaryotic Cells and Eukaryotic Cells

10 examples of friction in our daily life




