Question

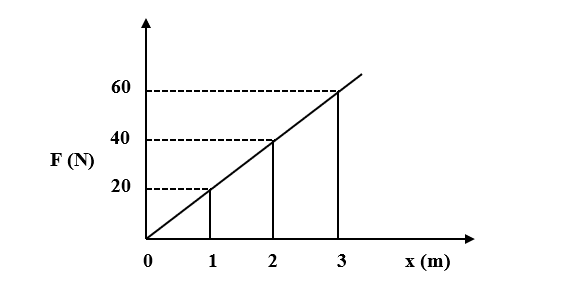
Calculate the work done in moving the object from x=2 to x=3 m from the given graph.

Answer 1

Hint: By looking at the graph we can say, the work done by the object for displacement from x=2 m to x=3 m will be equal to the area under the curve. The two parallel lines one from x= 2 and another from x=3 together with the line from the origin and the X-axis form a trapezium. So, the work done will be equal to the area of trapezium. Use the formula for the area of trapezium and find the area. This will be the value of work done.

Formula used:
$A= \dfrac {1}{2} \times sum\ of\ two\ parallel\ lines\times distance\ between\ the\ parallel\ lines$

Complete step-by-step solution:
Given:
Initial position ${x}_{initial}$= 2 m
Final position ${x}_{final}$= 3 m
We know, work done is given by,
$W= F.x$ …(1)
Where,
$F$ is the force
$x$ is the displacement
From the graph, we can see that the line from x=2 m intersects the line frm the origin at F= 40 N and the line from x=3 m intersects the line at F= 60 N.
$\Rightarrow { F }_{2 }=40N$ and ${ F }_{ 3 }=60N$
We can also infer that these two parallel lines one from x= 2 and another from x=3 together with the line from the origin and the X-axis form a shape of a trapezium.
So, using the equation. (1) and force vs displacement graph, we can say that the work done will be the area under the curve which is trapezium.
Thus, the work done will be,
$W= Area \ of \ a \ trapezium$ …(2)
Area of a trapezium is given by,
$A= \dfrac {1}{2} \times sum\ of\ two\ parallel\ lines\times distance\ between\ the\ parallel\ lines$
$\Rightarrow A= \dfrac {1}{2} \times \left( { F }_{ 2 }+{ F }_{ 3 } \right) \times \left( { x }_{ final }-{ x }_{ initial } \right)$
Substituting values in above equation we get,
Substituting values in above equation we get,
$A= \dfrac {1}{2} \times \left( 40+60 \right) \times \left( 3-2 \right)$
$\Rightarrow A= \dfrac {1}{2} \times 100 \times 1$
$\Rightarrow A= 50$
Substituting this value in the equation. (2) we get,
$W= 50 J$

So, the work done in moving the object from x=2 to x=3 m will be 50 J.

Note:
Work done is highly dependent on the displacement of a body no matter how much force is applied. If the displacement is zero then the work done remains zero. When we talk about the graph of force vs displacement, it means that the force is a function of displacement. Thus, the nature of the graph and its slope will depend upon the nature of the function.