Question

Calculate the steady current through the 2Ω resistor in the circuit shown below:

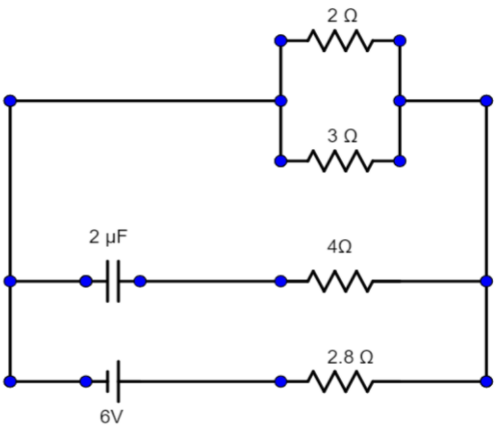
Answer 1

Hint: Steady current: It means, in a capacitive circuit (having one or more capacitors), which when operated over D.C, after a very short interval of time, the current in the branch of a circuit, containing a capacitor becomes zero. This happens because when we apply D.C voltage across a capacitor, it gets charged, and then it can’t accommodate more charge than that. Hence stops the flow of current.

Formula used:
Resistance in series: $R_{total}=R_1 +R_2+R_3+ . . .$
Resistance in parallel: $\dfrac 1{R_{total}} =\dfrac 1{R_{1}}+\dfrac 1{R_{2}}+\dfrac 1{R_{3}}.......$
Ohm’s law: $V=iR$

Complete step-by-step solution:
In the steady-state, the capacitor won’t allow the current to pass. Hence that branch of the circuit behaves as an open circuit hence there’s no effect of the branch on the circuit.

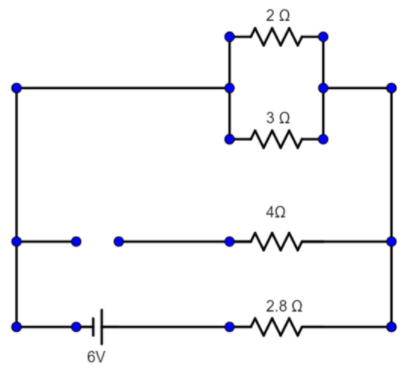
Now, as $2\Omega$ and $3\Omega$ resistor are in parallel. Hence using $\dfrac 1{R_{total}} =\dfrac 1{R_{1}}+\dfrac 1{R_{2}}$
$\dfrac 1{R_{total}} =\dfrac 1{2}+\dfrac 1{3}$
Or $R_{total} = \dfrac{3 \times 2}{3+2} = \dfrac 65 = 1.2 \Omega$
Hence the circuit can be redrawn as:

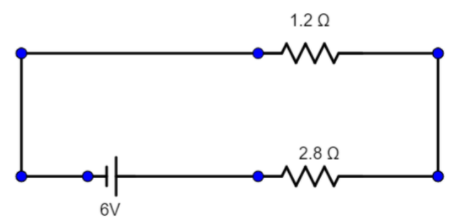
Now as $1.2\Omega$ and $2.8\Omega$ resistors are in series, hence we can use $R_{total}=R_1 +R_2= 1.2 + 2.8 = 4 \Omega$
Hence the circuit can be redrawn as:

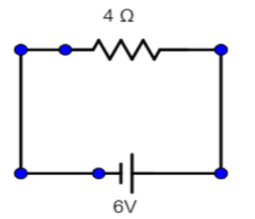
Now, using ohm’s law:
$V=iR$, where R is the total resistance
$6 = i \times 4$
Or $i = \dfrac{6}{4} = 1.5 A$
Now, the current through $1.2\Omega$ resistor is $1.5A$ in

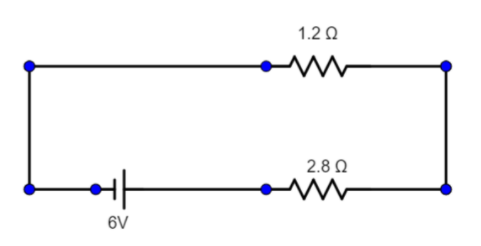
Hence $V_{1.2\Omega } = 1.2 \times 1.5 = 1.8V$ [Using ohm’s law]
Now since we need the current through $2\Omega$ resistor and, $3\Omega$ and $2\Omega$ resistors are in parallel, hence have the same potential difference.

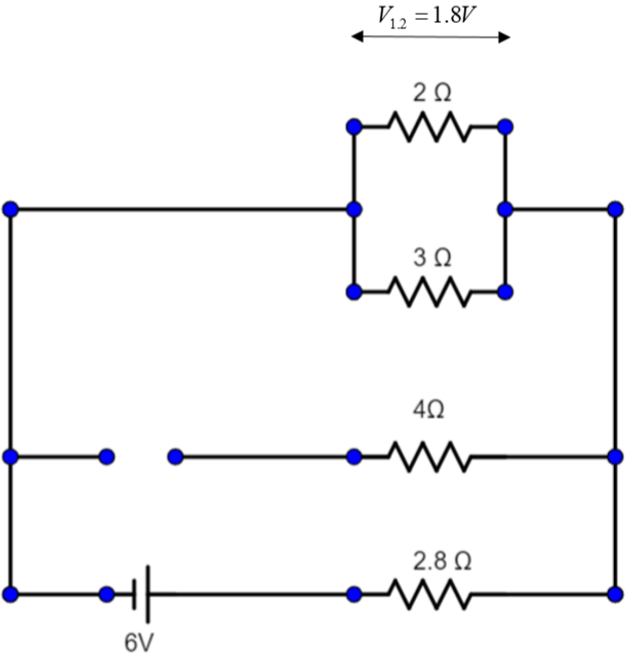
Now, since the potential difference across $2\Omega$ resistor is $1.8V$, hence current:
$i=\dfrac {1.8}{2} = 0.9 A$
So, current through $2\Omega$ resistor is 0.9A.

Note: Students must be comfortable with circuits like what is series and what is parallel. This can only be achieved through a lot of practice. Also if instead of D.C we would have taken A.C, then we can’t open the circuit like this for capacitors. One can also apply Kirchhoff’s law for finding the potential difference between any two points in a circuit.