Question

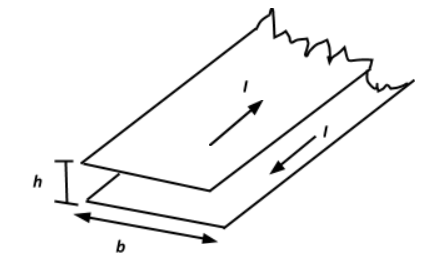
Calculate the inductance of unit length of a double tape line as shown in the figure. The tapes are separated by a distance h which is considerably less than their width b.

A) \[\dfrac{{{\mu _0}h}}{b}\]
B) \[\dfrac{{{\mu _0}h}}{{2b}}\]
C) \[\dfrac{{2{\mu _0}h}}{b}\]
D) \[\dfrac{{\sqrt 2 {\mu _0}h}}{b}\]

Answer 1

Hint:To find the required inductance per unit length of a double tape line we have to figure out the magnetic field within the interior region of the double tape with the help of ampere-circuital law after that we will calculate the magnetic flux link with the magnetic field within its interior region. Finally, we use the formula in order to calculate the magnetic inductance as: \[L = \dfrac{\phi }{I}\], where \[L\] is the inductance \[\phi \] is the magnetic flux and \[I\] is the current.

Complete step-by-step answer:
To calculate the required inductance per unit length of the double tape we apply ampere-circuital law first.

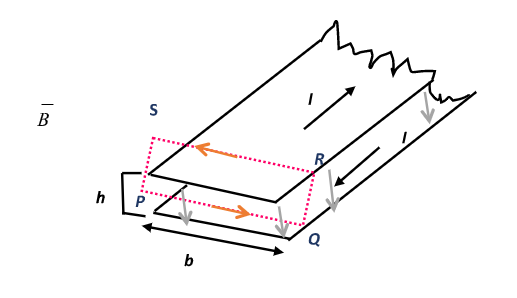
Let us consider the amperian- loop PQRS as shown above. The line PQ is parallel to the length b and also parallel to the magnetic field \[\vec B\] within the interior region in between the tape while the line QR and PS are perpendicular to \[\vec B\].
Applying ampere-circuital law:
\[Bb + 0 + Bb + 0 = {\mu _0}I\] (Along line QR and SP \[\vec B\] and \[d\vec l\] are perpendiculars so there dot product are also zero)
\[ \Rightarrow 2Bb = {\mu _0}I\]
\[ \Rightarrow B = \dfrac{{{\mu _0}I}}{{2b}}\]
Similarly, the magnetic field due to lower surface \[B = \dfrac{{{\mu _0}I}}{{2b}}\]
Now, total magnetic field \[{B_T} = 2 \times \dfrac{{{\mu _0}I}}{{2b}}\]
\[ \Rightarrow {B_T} = \dfrac{{{\mu _0}I}}{b}\]
Magnetic flux link with \[{B_T}\]will be written as-
\[\phi = {B_T} \times Area\]
As
So,
 \[ \Rightarrow \phi = \dfrac{{{\mu _0}Ilh}}{b}\]
Calculating inductance as
\[L = \dfrac{\phi }{I}\]……………(i)
Substitute the value of \[\phi = \dfrac{{{\mu _0}Ilh}}{b}\] in the equation (i) we get
\[L = \dfrac{{{\mu _0}lh}}{b}\]
Now, we calculate the required inductance per unit length.
\[\dfrac{L}{l} = \dfrac{{{\mu _0}h}}{b}\].
Thus the inductance per unit length of a double tape line\[\left( {\dfrac{L}{l}} \right) = \dfrac{{{\mu _0}h}}{b}\]
Hence, Option (A) is the correct answer.

Note: In order to answer such kinds of conceptual questions students must have conceptual clarity of the Ampere-circuital law. Along with that, one should have the ability to relate a link between the concept behind the laws and its implementation while solving the conceptual problems. One should also remember the various fact-based short formulas and their implementation while solving tricky numerical problems.