Question

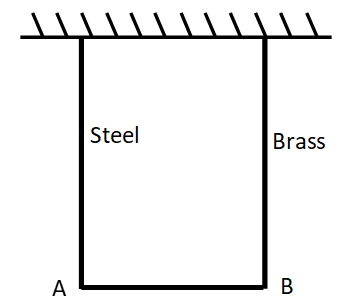
Calculate the diameter of the brass wire.

A. $2.1 \times {10^{ - 4}}m$
B. $4.2 \times {10^{ - 4}}m$
C. $8.4 \times {10^{ - 4}}m$
D. $16.8 \times {10^{ - 4}}m$

Answer 1

Hint: Correction if the question calculates the diameter of brass wire. Given diameter of steel wire is $0.6mm$ and $\dfrac{{{y_b}}}{{{y_s}}} = \dfrac{1}{2} $ . Since the weight AB are equally distributed in both wires, the strain will be the same in both i.e. ratio of stress to young's modulus of elasticity will be constant.
(1) $\dfrac{{Stress}}{{Young's{\text{ modules}}}} = cons\tan t$
(2) Area of base of wire $ = \pi {r^2}$
Where r is the radius of base.

Complete step by step answer:
Since both the wires i.e. steel and brass are subjected to weight AB this weight will produce elongation in the wire.
The ratio of longitudinal stress as the longitudinal strain within the elastic limit is known as young’s modulus of elasticity, Y.
Now, as the weight is equally distributed on both wires, so the strain in both the wires will be the same.
Now, young’s modulus, $Y = \dfrac{{Stress}}{{Strain}}$
$ \Rightarrow \dfrac{{Stress}}{Y} = Strain$
As strain is same, it can be treated constant here
So, $\dfrac{{Stress}}{Y} = Cons\tan t$
$ \Rightarrow {\left( {\dfrac{{Stress}}{Y}} \right)_{brass}} = {\left( {\dfrac{{Stress}}{Y}} \right)_{steel}}$…. (i)
Now, stress $ = \dfrac{{Force}}{{Area}}$
And, Area $ = \pi {r^2}$… (Where r is radius of wire)
So, stress $ = \dfrac{{Force}}{{\pi {r^2}}}$
Also, since weights are equally distributed, force will also be the same in both.
So, equation (i) become
$
  \dfrac{{Force}}{{{{\left( {Area} \right)}_{brass}} \times {Y_b}}} = \dfrac{{Force}}{{{{\left( {Area} \right)}_{steel}} \times {Y_s}}} \\
   \Rightarrow \dfrac{1}{{\pi r_b^2 \times {Y_b}}} = \dfrac{1}{{\pi r_s^2 \times {Y_s}}} \\
 $
Where, ${Y_b}$ is young’s modulus for brass and ${Y_s}$ is young’s modulus for steel
Also, ${r_b}$ is radius of brass and ${r_s}$ is radius of steel $ = \dfrac{{0.6}}{2} = 0.3m$
$ = 0.3 \times {10^{ - 3}}$
$
   \Rightarrow \dfrac{1}{{r_b^2 \times {Y_b}}} = \dfrac{1}{{r_s^2 \times {Y_s}}} \\
   \Rightarrow \dfrac{1}{{r_b^2}} = \dfrac{{{Y_b}}}{{{Y_s}}} \times \dfrac{1}{{r_s^2}} \\
   \Rightarrow \dfrac{1}{{r_b^2}} = \dfrac{1}{2} \times \dfrac{1}{{{{\left( {0.3 \times {{10}^{ - 3}}} \right)}^2}}} \\
   \Rightarrow r_b^{} = \sqrt {2 \times {{\left( {0.3 \times {{10}^{ - 3}}} \right)}^2}} \\
   \Rightarrow {r_b} = 1.414 \times 0.3 \times {10^{ - 3}} = 0.424m \times {10^{ - 3}} \\
 $
So, diameter of brass $ = 2 \times 0.4242 \times {10^{ - 3}}$
$ = 0.8484 \times {10^{ - 3}}$
$ = 8.4 \times {10^{ - 4}}m$

So, the correct answer is “Option C”.

Note:
Here $ Area = {\pi r^2} $ because the area is to be taken where the force acts. As the force acts on the base of wire. So, the area of the base which is circular in shape is taken.