
Between which two points of the concave mirror should an object be placed to obtain a magnification of:
(a) -3 (b) +2.5 (c) -0.4
Answer
535.8k+ views
Hint: The magnification of the mirror is the size of the image by the size of the object. The magnification can also be defined as the distance of the image by the distance of the object. Using the properties of the magnification of the concave mirror we will be solving the problem.
Formula used:
\[\begin{align}
& m=-\dfrac{v}{u} \\
& m=\dfrac{v}{-u} \\
\end{align}\]
Complete answer:
From the given information, we have the data as follows.
The magnification of a spherical mirror is the ratio of the size of the image formed by the mirror to the size of the object.
In the case of the concave mirror, when the image formed is real, the magnification will be negative. Similarly, when the image formed is virtual, the magnification will be positive. If the magnification is negative, the image formed will be real, inverted and enlarged.
For the magnification value of -3, the image formed will be real, inverted and enlarged/magnified. The object must be placed between the principal focus F and the centre of curvature C of the concave mirror.
The ray diagram representing the object placed between the principal focus F and the centre of curvature C of the concave mirror.
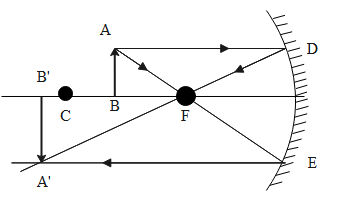
For the magnification value of +2.5, the image formed will be virtual and erect. The object must be placed between the pole and the principal focus (F) of the concave mirror.
The ray diagram representing the object placed between the pole and the principal focus (F) of the concave mirror.
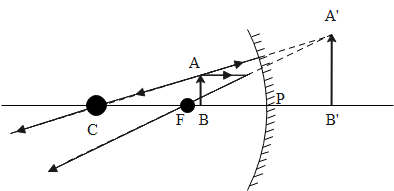
For the magnification value of -0.4, the image formed will be real, inverted and diminished. The object must be placed beyond the centre of curvature C of the concave mirror.
The ray diagram representing the object placed beyond the centre of curvature C of the concave mirror.
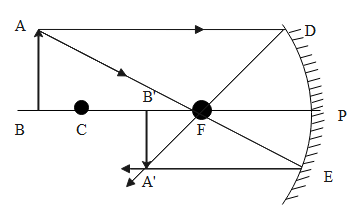
The mirror table of the concave mirror.
\[\therefore \] The magnification of: (a) -3, the object should be placed between the principal focus F and the centre of curvature C (b) +2.5, the object should be placed between the pole and the principal focus (F) (c) -0.4, the object should be placed beyond the centre of curvature.
Note:
The magnification is also called linear magnification. In the case of a convex mirror, the magnification will be positive.
Formula used:
\[\begin{align}
& m=-\dfrac{v}{u} \\
& m=\dfrac{v}{-u} \\
\end{align}\]
Complete answer:
From the given information, we have the data as follows.
The magnification of a spherical mirror is the ratio of the size of the image formed by the mirror to the size of the object.
In the case of the concave mirror, when the image formed is real, the magnification will be negative. Similarly, when the image formed is virtual, the magnification will be positive. If the magnification is negative, the image formed will be real, inverted and enlarged.
For the magnification value of -3, the image formed will be real, inverted and enlarged/magnified. The object must be placed between the principal focus F and the centre of curvature C of the concave mirror.
The ray diagram representing the object placed between the principal focus F and the centre of curvature C of the concave mirror.

For the magnification value of +2.5, the image formed will be virtual and erect. The object must be placed between the pole and the principal focus (F) of the concave mirror.
The ray diagram representing the object placed between the pole and the principal focus (F) of the concave mirror.

For the magnification value of -0.4, the image formed will be real, inverted and diminished. The object must be placed beyond the centre of curvature C of the concave mirror.
The ray diagram representing the object placed beyond the centre of curvature C of the concave mirror.

The mirror table of the concave mirror.
| Object location | Large or small | Virtual or real | Inverted or erect | Position |
| Beyond 2F | Small | Real | Inverted | Between F and 2F |
| At 2F | Same | Real | Inverted | At 2F |
| Between 2F and F | Large | Real | Inverted | Beyond 2F |
| Between F and the lens | Large | Virtual | Erect | Behind the mirror |
\[\therefore \] The magnification of: (a) -3, the object should be placed between the principal focus F and the centre of curvature C (b) +2.5, the object should be placed between the pole and the principal focus (F) (c) -0.4, the object should be placed beyond the centre of curvature.
Note:
The magnification is also called linear magnification. In the case of a convex mirror, the magnification will be positive.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




