Question

At the center of a fixed large circular coil of radius $R$, a much smaller circular coil of radius $r$ is placed. The two coils are concentric and are in the same plane. The larger coil carries a current $I$. The smaller coil is set to rotate with a constant angular velocity $\omega $ about an axis along their common diameter. Calculate the emf induced in the smaller coil after a time $t$ of its start of rotation.
A. $\dfrac{{{\mu _0}I}}{{2R}}\omega {r^2}\sin \omega t$
B. $\dfrac{{{\mu _0}I}}{{4R}}\omega \pi {r^2}\sin \omega t$
C. $\dfrac{{{\mu _0}I}}{{2R}}\omega \pi {r^2}\sin \omega t$
D. $\dfrac{{{\mu _0}I}}{{4R}}\omega {r^2}\sin \omega t$

Answer 1

Hint: First step will be to calculate the flux in touch with the smaller coil.
After its determination, we can find out the emf induced in it due to its rotation.

Formula used:
Flux in touch with the smaller coil: $\phi = \vec B.\vec A = BA\cos \theta $
Where $\phi $ is the change in magnetic flux in touch with the smaller coil and is expressed in Tesla $(T)$, $B$ is the intensity of magnetic field in touch with the smaller coil and is expressed in Webers $(W)$, $A$ is the area and is expressed in meter square $({m^2})$ and $\theta $ is the angle between the perpendicular area vector magnetic field and is expressed in radians $(rad)$.
Emf induced: $\varepsilon = - \dfrac{{d\phi }}{{dt}}$
Where $\varepsilon $ is the induced emf and is expressed in Volts $(V)$, \[d\phi \] is the change in magnetic flux in contact with the smaller coil and is expressed in Webers $(W)$ and $dt$ is the change in time and is expressed in seconds $(s)$.
Magnetic field induced by the larger coil: \[B = \dfrac{{{\mu _0}I}}{{2R}}\]
Where ${\mu _0}$ is the permittivity of vacuum \[(1approx)\], $I$ is the moment of inertia and is expressed I meter to the power four $({m^4})$ and $R$ is the radius of the outer coil and is expressed in meters $(m)$.

Complete step by step answer:

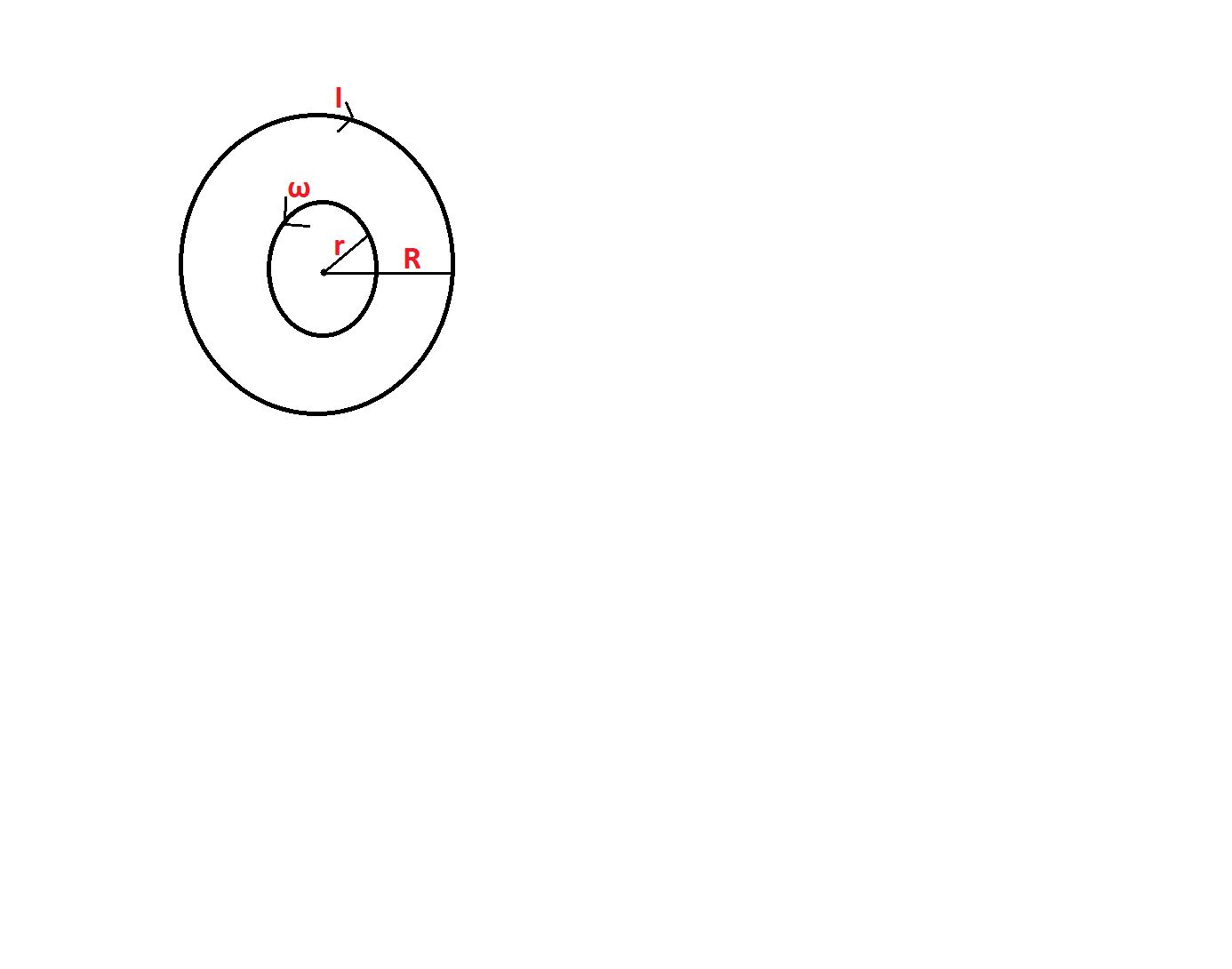
Due to the flow of current in the larger coil, a magnetic field $B$ will be produced around it. This field is in touch with the inner smaller coil which rotates with an angular velocity of $\omega $. Due to this continuous rotation there will be a change in the number of magnetic field force lines in contact with it. Therefore, a change in magnetic flux $d\phi $ will be observed with passage of time $dt$.
Now, value of magnetic flux in touch with the inner coil $ = \phi = \vec B.\vec A = BA\cos \theta $.
For our coil, the radius is and the angle $\theta $ is $\omega t$. Therefore the above expression becomes the following after substitution,
$\phi = BA\cos \theta = B\pi {r^2}\cos \omega t$
We know that the induced emf will be equal to the negative ratio of flux change with respect to time. That is, $\varepsilon = - \dfrac{{d\phi }}{{dt}}$.
Now, substituting the determined value of $\phi $ we get,
$\varepsilon = - \dfrac{{d\phi }}{{dt}} = - \dfrac{d}{{dt}}(B\pi {r^2}\cos \omega t)$.
But \[B = \dfrac{{{\mu _0}I}}{{2R}}\].
Therefore we get,
$\varepsilon = - \dfrac{d}{{dt}}(B\pi {r^2}\cos \omega t) = - \dfrac{d}{{dt}}(\dfrac{{{\mu _0}I}}{{2R}})(\pi {r^2}\cos \omega t)$
Upon differentiation we will get,
$\varepsilon = \dfrac{{{\mu _0}I}}{{2R}}\pi {r^2}\sin \omega t$.

So, the correct answer is “Option C”.

Note:
Emf induced is always a negative ratio of the change in flux with respect to time because the produced emf repels the cause that produces it. This is in accordance with Lenz’s Law. Therefore, it is always negative.