Question

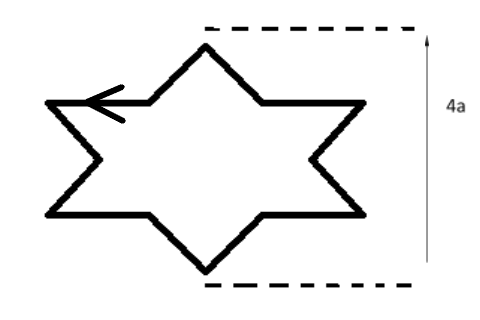
Asymmetric star shaped conducting wire loop is carrying a steady state current I as shown in the figure. The distance between the diametrically opposite vertices of the star is 4a. The magnitude of the magnetic field at the centre of the loop is :

a. $\dfrac{{{\mu _0}I}}{{4\pi a}}6\left[ {\sqrt 3 - 1} \right]$
b. $\dfrac{{{\mu _0}I}}{{4\pi a}}3\left[ {\sqrt 3 - 1} \right]$
c. $\dfrac{{{\mu _0}I}}{{4\pi a}}6\left[ {\sqrt 3 + 1} \right]$
d. $\dfrac{{{\mu _0}I}}{{4\pi a}}3\left[ {2 - \sqrt 3 } \right]$

Answer 1

Hint: Magnetic field due to current carrying conductor (here the conductor is given in the star shape in the question) is given by Ampere’s circuital law. In mathematical terms it is given as:
$\dfrac{{{\mu _0}I}}{{4\pi a}}\left( {\sin {\phi _1} + \sin {\phi _2}} \right)$
Here, $I$ is the current flowing in the conductor,
$a$ is the distance of magnetic field from the conductor and
${\phi _1}$ and ${\phi _2}$ are the angles which are observed in the figure.

Complete step by step answer:
Ampere’s circuital law states that: line integral of magnetic field surrounding a closed loop equals the number of times the algebraic sum of currents passing through the loop.
Now come to the calculation part:
Value of angles in which we observe in the figure given in the question is:
${60^0}$ and ${30^0}$
One triangle of the star is making 600 but in order to find the magnetic field due to the current carrying on the outer side of the triangle we will subtract angle 300 from the total angle.
Our expression will become as:
$
   \Rightarrow \dfrac{{{\mu _0}I}}{{4\pi a}}\left( {\sin {{60}^0} - \sin {{30}^0}} \right) \\
   \Rightarrow \dfrac{{{\mu _0}I}}{{4\pi a}}(\dfrac{{\sqrt 3 }}{2} - \dfrac{1}{2}) \\
 $ (We have substituted the values of both the angles) -----(1)
As the current loop has 12 sides we have calculated the magnetic field due to one side, so we will multiply the expression 1 by 12.
$
   \Rightarrow \dfrac{{{\mu _0}I}}{{4\pi a}} \times \dfrac{{12}}{2}\left[ {\sqrt 3 - 1} \right] \\
   \Rightarrow \dfrac{{{\mu _0}I}}{{4\pi a}}6\left[ {\sqrt 3 - 1} \right] \\
 $ (We have taken $\dfrac{1}{2}$ common and 12 is divided by 2).

Hence, the correct answer is option (A).

Note: Ampere circuital has a very well known application which is that the concept of Ampere’s circuital law is used by current carrying solenoid, for because of which magnetic induction is observed. Phenomenon of magnetic induction is used in transformers for linking the windings.