Question

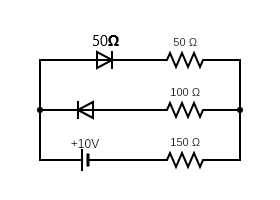
Assume that each diode shown in the figure has a forward bias resistance of $ 50\Omega $ and an infinite reverse bias resistance. The current through the resistance $ 150\Omega $ is

(A) $ 0.66{\text{A}} $
(B) $ {\text{0}}{\text{.05A}} $
(C) Zero
(D) $ {\text{0}}{\text{.04A}} $

Answer 1

Hint
A diode is said to be forward biased if the positive end of the cell or battery is connected to the positive terminal of the diode (triangularly shaped in schematics) and the negative terminal of the cell is connected to the negative terminal of the diode. We need to apply Kirchhoff’s voltage rule to the loop whose resistance isn’t infinite. From there we will get the current.
Formula used: In this solution we will be using the following formula,
 $ \sum V = 0 $ where $ V $ is the individual voltage around the loop.
 $ \Rightarrow V = IR $ where $ V $ is the voltage drop across a resistor, $ I $ is the current through the resistor and $ R $ is the resistance of the resistor.

Complete step by step answer
From the schematic diagram, it is obvious that one of the two diodes is reversed biased since they face opposite directions. Now, we need to recognize the forward biased diode and the reverse biased diode. A diode is forward biased if the positive end of the cell or battery is connected to the positive terminal of the diode and the negative terminal of the cell is connected to the negative terminal of the diode. We see from schematics that the positive terminal of the 10 V cell is connected to the positive terminal of the top diode. Hence, the top diode is forward biased.
So we can neglect the bottom loop (the middle wire) since the resistance is infinite. On applying the Kirchhoff’s voltage rule from the 10 V cell through the $ 50\Omega $ and $ 150\Omega $ resistors and $ 50\Omega $ resistance of the diode, we get
 $ \Rightarrow 10 - I\left( {50} \right) - I(50) - I\left( {150} \right) = 0 $
 $ \Rightarrow 10 = 250I $
Calculating for $ I $ by dividing both sides by 250, we have
 $ \Rightarrow I = \dfrac{{10}}{{250}} = 0.04{\text{A}} $
 $ \therefore I = 0.04{\text{A}} $
Hence, the correct option is (B).

Note
In actuality, the reverse resistance of a reverse biased diode is not infinite. In fact, small reverse current does flow through due to minority carriers. However, in most cases, they are negligible, usually of the order of $ {\text{1}}{{\text{0}}^{ - 6}}{\text{A}} $.