
Assertion
The linear equations $x - 2y - 3 = 0$ and $3x + 4y - 20 = 0$ have exactly one solution.
Reason
The linear equations $2x + 3y - 9 = 0$ and $4x + 6y - 18 = 0$have a unique solution
A. Both assertion and reason are correct and the reason is the correct explanation for assertion
B. Both assertion and reason are correct but the reason is not the correct explanation for assertion
C. The assertion is correct but the reason is incorrect
D. The assertion is incorrect but the reason is correct
Answer
576.6k+ views
Hint: We have been given two different statements in the assertion and the reason so we’ll check for them separately, in both the cases we’ll find the number of solutions for the given linear equations. After that, we’ll check with the given options.
Complete step by step answer:
for assertion
solving for the linear equations $x - 2y - 3 = 0$ and $3x + 4y - 20 = 0$
$ \Rightarrow 3x + 4y - 20 = 0.............(i)$
$ \Rightarrow x - 2y - 3 = 0...............(ii)$
$ \Rightarrow x = 2y + 3$
Substituting the value of ‘x’ in equation(i)
$ \Rightarrow 3(2y + 3) + 4y - 20 = 0$
Simplifying the brackets
$ \Rightarrow 6y + 9 + 4y - 20 = 0$
Simplifying the like terms
$ \Rightarrow 10y - 11 = 0$
$ \Rightarrow y = \dfrac{{11}}{{10}}$
Substituting the value of ‘y’ in equation(ii)
$ \Rightarrow x - 2\left( {\dfrac{{11}}{{10}}} \right) - 3 = 0$
Simplifying by grouping the like terms
$ \Rightarrow x = 2\left( {\dfrac{{11}}{{10}}} \right) + 3$
$\therefore x = \dfrac{{26}}{5}$
Since we got a single solution i.e. $\left( {\dfrac{{11}}{{10}},\dfrac{{26}}{5}} \right)$
Therefore the given equations have only one solution
for reason
solving for the linear equations $2x + 3y - 9 = 0$ and $4x + 6y - 18 = 0$
$ \Rightarrow 2x + 3y - 9 = 0..........(iii)$
$ \Rightarrow 4x + 6y - 18 = 0...........(iv)$
Dividing equation(iv) by 2
$ \Rightarrow 2x + 3y - 9 = 0$
From the above equations, we can say that both the equations of the line are the same or we can say that both the line coinciding
Since the lines are coinciding, then we’ll have an infinite number of solutions.
Now, from the above results, we can say that assertion is correct but reason id not true
Option(C) is correct.
Note: We can also verify our solution with the help of graph plotting
Assertion
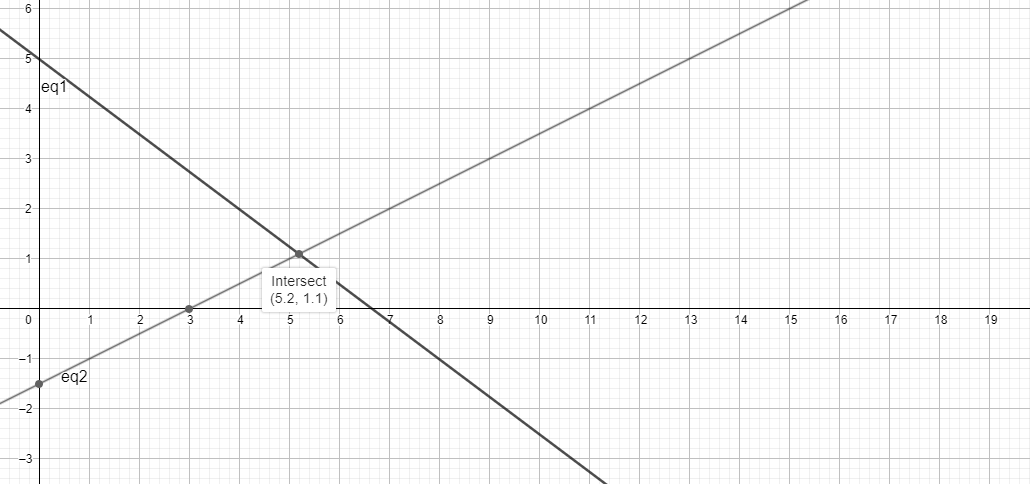
Reason
Since both lines coincide,
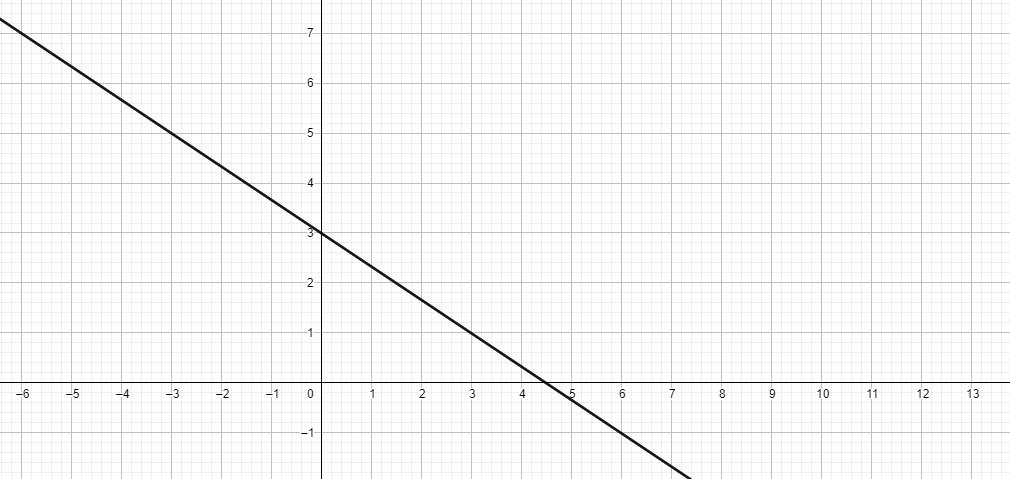
Complete step by step answer:
for assertion
solving for the linear equations $x - 2y - 3 = 0$ and $3x + 4y - 20 = 0$
$ \Rightarrow 3x + 4y - 20 = 0.............(i)$
$ \Rightarrow x - 2y - 3 = 0...............(ii)$
$ \Rightarrow x = 2y + 3$
Substituting the value of ‘x’ in equation(i)
$ \Rightarrow 3(2y + 3) + 4y - 20 = 0$
Simplifying the brackets
$ \Rightarrow 6y + 9 + 4y - 20 = 0$
Simplifying the like terms
$ \Rightarrow 10y - 11 = 0$
$ \Rightarrow y = \dfrac{{11}}{{10}}$
Substituting the value of ‘y’ in equation(ii)
$ \Rightarrow x - 2\left( {\dfrac{{11}}{{10}}} \right) - 3 = 0$
Simplifying by grouping the like terms
$ \Rightarrow x = 2\left( {\dfrac{{11}}{{10}}} \right) + 3$
$\therefore x = \dfrac{{26}}{5}$
Since we got a single solution i.e. $\left( {\dfrac{{11}}{{10}},\dfrac{{26}}{5}} \right)$
Therefore the given equations have only one solution
for reason
solving for the linear equations $2x + 3y - 9 = 0$ and $4x + 6y - 18 = 0$
$ \Rightarrow 2x + 3y - 9 = 0..........(iii)$
$ \Rightarrow 4x + 6y - 18 = 0...........(iv)$
Dividing equation(iv) by 2
$ \Rightarrow 2x + 3y - 9 = 0$
From the above equations, we can say that both the equations of the line are the same or we can say that both the line coinciding
Since the lines are coinciding, then we’ll have an infinite number of solutions.
Now, from the above results, we can say that assertion is correct but reason id not true
Option(C) is correct.
Note: We can also verify our solution with the help of graph plotting
Assertion

Reason
Since both lines coincide,

Recently Updated Pages
Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




