Question

Assertion: Angle of repose is equal to the angle of limiting friction.
Reason: When the body is just about to move, the force of friction in this stage is called the limiting friction.
A. Both Assertion and Reason are correct and Reason is the correct explanation for Assertion
B. Both Assertion and Reason are correct but Reason is not the correct explanation for Assertion
C. Assertion is correct but Reason is incorrect
D. Assertion is incorrect but Reason is correct.

Answer 1

Hint: Firstly, we will define all the parameters used in the explanation. Then, we will check for the correctness of the assertion statement, followed by the checking of the correctness of the reason statement. Then, we will find out the relation between the assertion and the reason.

Complete answer:
The definitions of the parameters used are as follows:

The angle of repose: the maximum angle of inclination such that the body placed on an inclined plane remains at rest.

The angle of limiting friction: the angle between the normal reaction and the resultant force.

The force of friction: the force that opposes the motion of the body.

The limiting friction: the maximum value of the static fraction that comes into play just before the body starts to move over the surface of the other body.

Firstly, we will consider the assertion statement, that is, Assertion: Angle of repose is equal to the angle of limiting friction.

Consider the free body diagram of a block placed on an inclined plane.

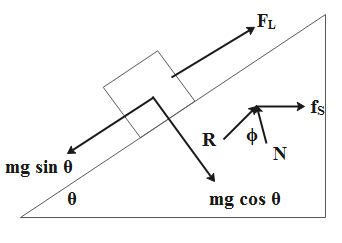
From the above free body diagram, it’s clear that,

The normal force is given as follows.

\[N=mg\cos \theta \]…… (1)

The force of limiting friction, that is, the frictional force is given as follows.

\[{{f}_{S}}={{\mu }_{S}}N\]…… (2)

From the free body diagram, we will equate the forces such as below.

\[mg\sin \theta ={{f}_{S}}\]

Equate the equation (2) in the above equation.

\[mg\sin \theta ={{\mu }_{S}}N\]

Substitute the equation (1) in the above equation

\[mg\sin \theta ={{\mu }_{S}}mg\cos \theta \]

Continue the further calculation, thus, the angle of friction is,

\[{{\mu }_{S}}=\tan \theta \]…… (A)

Now, in the case of frictional force and the normal force, we have,

\[\begin{align}
  & \tan \phi =\dfrac{{{f}_{S}}}{N} \\
 & \tan \phi =\dfrac{{{\mu }_{S}}N}{N} \\
\end{align}\]

Therefore, the angle of repose is,

\[\tan \phi ={{\mu }_{S}}\]…… (B)

Comparing the equations (A) and (B) it’s clear that,

\[\begin{align}
  & \tan \phi =\tan \theta \\
 & \Rightarrow \phi =\theta \\
\end{align}\]

The angle of repose equals the angle of limiting friction.

Secondly, we will consider the reason statement, that is, Reason: When the body is just about to move, the force of friction in this stage is called the limiting friction.

Consider the free body diagram of a block placed on an inclined plane.

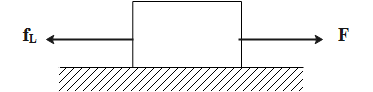
From the above figure, it’s clear that,

\[{{f}_{L}}=F\]

It is always true that, when, the body is about to start the motion, the force of friction equals the limiting friction.

\[\therefore \] The statements of the assertion and the reason are correct. But, the reason is not the correct explanation for the assertion.

As, both Assertion and Reason are correct but Reason is not the correct explanation for Assertion, thus, the option (B) is correct.

Note:
It becomes easy to understand the concepts like these, that is, the relation between the forces by drawing the free body diagram. As the free body diagrams help to clearly understand the number and the direction of forces acting on a body at a time.