
As the switch ‘S’ is closed in the circuit shown in the figure, the current passing through it is:
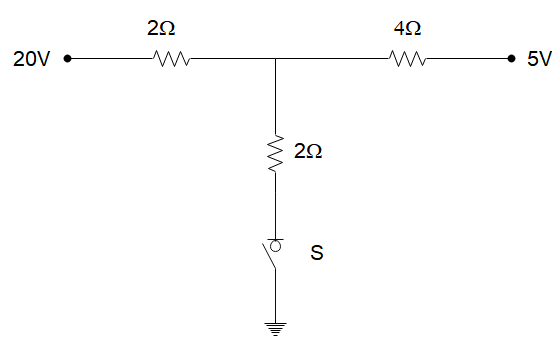
A) 5 A
B) 6 A
C) 3 A
D) zero

Answer
568.8k+ views
Hint : In this solution, we will use Kirchhoff's current law which helps us relate the current entering and leaving a junction. Further using ohm’s law we will be able to determine the current passing through the switch.
Formula used: In this solution, we will use the following formula:
Kirchhoff’s current law (KCL): $ \Sigma i = 0 $ at a junction
Ohm’s law: $ V = IR $ where $ V $ is the potential difference between two points between which current $ I $ is flowing through a resistor $ R $
Complete step by step answer
Let us start by assuming a potential $ V $ at the junction of the three cables as shown in the image below:
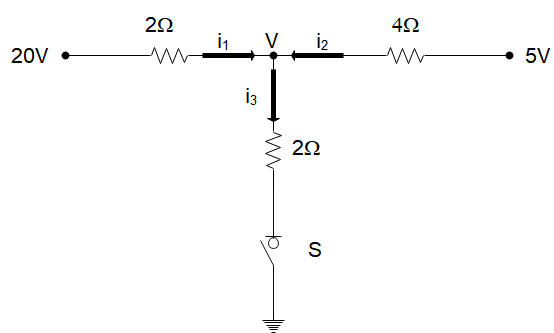
Let us also assume that the branch of 20 V current will have current $ {i_1} $ flowing through it, the branch of 5 V will have current $ {i_2} $ and the grounded branch will have current $ {i_3} $ . Then from Kirchhoff’s current law, we can write
$\Rightarrow {i_1} + {i_2} - {i_3} = 0 $
Then from ohm’s law, we can write $ i = \Delta V/R $ where $ \Delta V $ is the potential difference between two points of the branch
$\Rightarrow \dfrac{{20 - V}}{2} + \dfrac{{5 - V}}{4} - \dfrac{{V - 0}}{2} = 0 $
$\Rightarrow \dfrac{{40 - 2V}}{4} + \dfrac{{5 - V}}{4} - \dfrac{{2V}}{4} = 0 $
Taking an LCM of 4 we get,
$\Rightarrow \dfrac{{40 - 2V + 5 - V - 2V}}{4} = 0 $
$ \Rightarrow 45 - 5V = 0 $
Solving for $ V $ , we get
$\Rightarrow V = 9\,V $
Then the current through the switch will be
$\Rightarrow {i_3} = \dfrac{{V - 0}}{2} $
$ \Rightarrow {i_3} = 9/2\,A \approx 5A $
Hence the current flowing in the switch will be $ 5A $ which corresponds to option (A).
Note
Here we can intuitively observe that the potential of the junction point will be lower than the potentials at point A and B since current will be flowing from A and B towards the grounded branch and as a result, there will be a potential drop across the resistors causing the junction to have less potential than A and B. The sign of $ {i_3} $ will be opposite while using the KCL as it is flowing away from the junction and not towards it.
Formula used: In this solution, we will use the following formula:
Kirchhoff’s current law (KCL): $ \Sigma i = 0 $ at a junction
Ohm’s law: $ V = IR $ where $ V $ is the potential difference between two points between which current $ I $ is flowing through a resistor $ R $
Complete step by step answer
Let us start by assuming a potential $ V $ at the junction of the three cables as shown in the image below:

Let us also assume that the branch of 20 V current will have current $ {i_1} $ flowing through it, the branch of 5 V will have current $ {i_2} $ and the grounded branch will have current $ {i_3} $ . Then from Kirchhoff’s current law, we can write
$\Rightarrow {i_1} + {i_2} - {i_3} = 0 $
Then from ohm’s law, we can write $ i = \Delta V/R $ where $ \Delta V $ is the potential difference between two points of the branch
$\Rightarrow \dfrac{{20 - V}}{2} + \dfrac{{5 - V}}{4} - \dfrac{{V - 0}}{2} = 0 $
$\Rightarrow \dfrac{{40 - 2V}}{4} + \dfrac{{5 - V}}{4} - \dfrac{{2V}}{4} = 0 $
Taking an LCM of 4 we get,
$\Rightarrow \dfrac{{40 - 2V + 5 - V - 2V}}{4} = 0 $
$ \Rightarrow 45 - 5V = 0 $
Solving for $ V $ , we get
$\Rightarrow V = 9\,V $
Then the current through the switch will be
$\Rightarrow {i_3} = \dfrac{{V - 0}}{2} $
$ \Rightarrow {i_3} = 9/2\,A \approx 5A $
Hence the current flowing in the switch will be $ 5A $ which corresponds to option (A).
Note
Here we can intuitively observe that the potential of the junction point will be lower than the potentials at point A and B since current will be flowing from A and B towards the grounded branch and as a result, there will be a potential drop across the resistors causing the junction to have less potential than A and B. The sign of $ {i_3} $ will be opposite while using the KCL as it is flowing away from the junction and not towards it.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




