
As observed from the top of a 60 m high lighthouse from the sea level, the angles of depression of 2 ships are 30° and 45° if one ship is exactly behind the other on the same side of the light house. Find the distance between the two ships?
(a) 20m
(b) 43.92m
(c) 54.9m
(d) 60.1m
Answer
511.8k+ views
Hint:First draw the figure according to the statements given in question then use tan 30° and tan 45° to find the distance of the ships from the light house then subtraction of the distance of the two ships from the lighthouse is equal to distance between the ships.
Complete step-by-step answer:
In the below figure, AB is the length of the lighthouse, point C and E are the ships. BC is the distance of the first ship from the lighthouse and BE is the distance of the second ship from the lighthouse and CE is the distance between the ships.
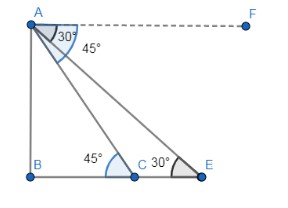
It is given that the length of the light house is 60m so AB = 60m. Angle of depression of the ship at point E is 30° and the angle of depression of the ship at point C is 45°.
Now, we are going to find the distance of the ships from the lighthouse.
Distance of the ship at point E from the lighthouse (BE) is calculated below:
In right angled $\Delta ABE$,
$\begin{align}
& \tan {{30}^{0}}=\dfrac{AB}{BE} \\
& \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{60}{BE} \\
& \Rightarrow BE=60\sqrt{3} \\
\end{align}$
So, the distance of the ship at point E from the lighthouse is 60√3m.
Distance of the ship at point C from the lighthouse (CB) is calculated below:
In right angled $\Delta ABC$,
$\begin{align}
& \tan {{45}^{0}}=\dfrac{AB}{BC} \\
& \Rightarrow 1=\dfrac{60}{BC} \\
& \Rightarrow BC=60 \\
\end{align}$
So, the distance of the ship at point C from the lighthouse is 60m.
Now, distance between the ships (CE) is equal to the difference of the distance of the ship from the lighthouse at point C and distance of the ship from the lighthouse at E (BE – BC).
BE – BC = 60√3 – 60
= 60(1.732 – 1)
= 60(0.732)
= 43.92
Hence, the distance between the two ships is 43.92m.
Hence, the correct option is (b).
Note: Angle of depression is always the angle from the horizontal line to the line of sight of the observer to the object. The angle of depression for the ship at point E is the angle between AF and AE for the ship at point E and angle of depression for ship at point C is the angle between AF and AC.
Don’t confuse the angle of depression as the angle between the lighthouse and the line of sight of an observer from the lighthouse to the ship. The angle of depression of the ship at point E is not the angle between AB and AE.
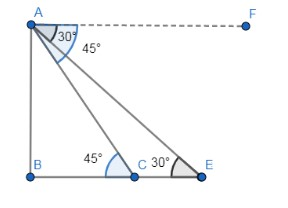
Complete step-by-step answer:
In the below figure, AB is the length of the lighthouse, point C and E are the ships. BC is the distance of the first ship from the lighthouse and BE is the distance of the second ship from the lighthouse and CE is the distance between the ships.

It is given that the length of the light house is 60m so AB = 60m. Angle of depression of the ship at point E is 30° and the angle of depression of the ship at point C is 45°.
Now, we are going to find the distance of the ships from the lighthouse.
Distance of the ship at point E from the lighthouse (BE) is calculated below:
In right angled $\Delta ABE$,
$\begin{align}
& \tan {{30}^{0}}=\dfrac{AB}{BE} \\
& \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{60}{BE} \\
& \Rightarrow BE=60\sqrt{3} \\
\end{align}$
So, the distance of the ship at point E from the lighthouse is 60√3m.
Distance of the ship at point C from the lighthouse (CB) is calculated below:
In right angled $\Delta ABC$,
$\begin{align}
& \tan {{45}^{0}}=\dfrac{AB}{BC} \\
& \Rightarrow 1=\dfrac{60}{BC} \\
& \Rightarrow BC=60 \\
\end{align}$
So, the distance of the ship at point C from the lighthouse is 60m.
Now, distance between the ships (CE) is equal to the difference of the distance of the ship from the lighthouse at point C and distance of the ship from the lighthouse at E (BE – BC).
BE – BC = 60√3 – 60
= 60(1.732 – 1)
= 60(0.732)
= 43.92
Hence, the distance between the two ships is 43.92m.
Hence, the correct option is (b).
Note: Angle of depression is always the angle from the horizontal line to the line of sight of the observer to the object. The angle of depression for the ship at point E is the angle between AF and AE for the ship at point E and angle of depression for ship at point C is the angle between AF and AC.
Don’t confuse the angle of depression as the angle between the lighthouse and the line of sight of an observer from the lighthouse to the ship. The angle of depression of the ship at point E is not the angle between AB and AE.

Recently Updated Pages
The largest wheat producing state in India is a Uttar class 12 biology CBSE

When a Hydrogen atom emits a photon of energy 1209eV class 12 physics CBSE

What chemical process is used for obtaining a metal class 12 chemistry CBSE

Assertion Sucrose is a nonreducing sugar Reason It class 12 chemistry CBSE

Find the maximum area of an isosceles triangle inscribed class 12 maths CBSE

Derive the expression for power P VI in an electrical class 12 physics CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers




