Question

As observed from the top of 100m height high lighthouse from the sea level the angle of depression of 2 ships are $30^\circ$ and $45^\circ$. If one ship is exactly behind the other on the same side of the light house. Find the distance between the two ships.

Answer 1

Hint: This question is again a common type of question form the height and distance. First draw the suitable diagram showing all the terms and their values. Then consider two right angled triangles one by one. In each triangle apply a suitable trigonometry ratio. First we'll make and sketch the giving situation. Then after that by using trigonometry property we will find different parameters and we will use two different triangles while taking one angle as reference for another.

Complete step-by-step answer:
First we draw the diagram as below. Top position of the light house is point A. Two ships are at point D and point C.

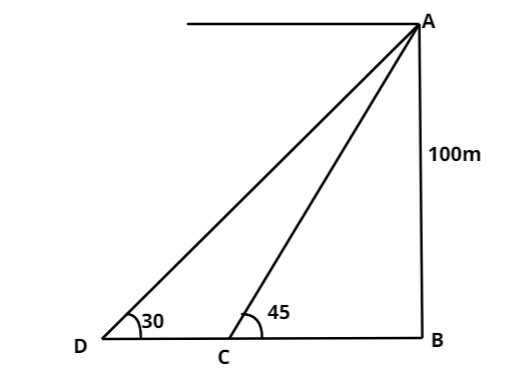
Let us suppose that the distance between two ships means the length of the CD is x meter.
Now, in right angle triangle ABC, we have
$
  \tan \angle ACB = \dfrac{{Perpendicular}}{{Base}} \\
   \Rightarrow \tan \angle ACB = \dfrac{{AB}}{{BC}} \\
 $
Substituting the values in above equation, we get
$ \Rightarrow \tan {45^ \circ } = \dfrac{{100}}{{BC}}$
As, $\tan {45^0} = 1$ , so we have
 $
   \Rightarrow 1 = \dfrac{{100}}{{BC}} \\
   \Rightarrow BC = 100 \\
 $ ….(1)
Now, in the right angled triangle ABD, we have
$
  \tan \angle ADB = \dfrac{{Perpendicular}}{{Base}} \\
   \Rightarrow \tan \angle ADB = \dfrac{{AB}}{{BD}} \\
 $
Substituting the values in above equation, we get
$ \Rightarrow \tan {30^ \circ } = \dfrac{{100}}{{BD}}$
As, $\tan {30^0} = \dfrac{1}{{\sqrt 3 }}$ , so we have
$ \Rightarrow \tan {30^ \circ } = \dfrac{{100}}{{BD}}$ …(2)
From the diagram we see that, BD = DC + BC
So, BD = x + 100 (from equation 1 put value of BC and also DC is assumed as x)
So, we have now in equation (2),
$
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{100}}{{BD}} \\
   \Rightarrow x + 100 = 100 \times \sqrt 3 \\
   \Rightarrow x = 100\sqrt 3 - 100 \\
   \Rightarrow x = 100(\sqrt 3 - 1) \\
   \Rightarrow x = 100 \times 0.732 \\
   \Rightarrow x = 73.2m \\
 $

$\therefore $Distance between the two ships will be 73.2 m.

Note: For geometrical shapes, especially in triangles, trigonometry ratios are very much applicable, for making relationships among the sides and angles of the triangle. There are six such trigonometry ratios have been defined. These are $\sin \theta ,\;\cos \theta ,\;\tan \theta ,\;\sec \theta ,\;\cos ec\theta ,\;and\;\cot \theta .$Also, angle of depression will always be equal to corresponding angle of elevation.