Question

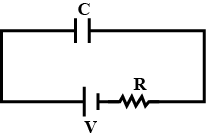
As an figure, it a capacitor of capacitance 'c' is charged by connecting it with resistance R, the energy given by the battery will be

A. \[\frac{1}{2}C{{V}^{2}}\]
B. less than \[\frac{1}{2}C{{V}^{2}}\]
C. \[C{{V}^{2}}\]
D. More than \[\frac{1}{2}C{{V}^{2}}\]

Answer 1

Hint: In the given figure, the capacitance C and resistance R connected to a potential difference of N. The capacitor is charged with resistance R then we have to calculate the energy of the battery.

Complete answer:
A capacitor of capacitance ‘C’ is Charged by connecting it with resistance R then energy of battery is given by
\[{{U}_{\max }}=\frac{1}{2}C{{V}^{2}}\]
As we know that the capacitor is a device of charge storing within it. So the maximum Stored by the capacitor is given by
\[{{U}_{\max }}=\frac{1}{2}C{{V}^{2}}\]
Where C = capacitance
And V = potential

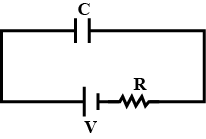
Now, when a capacitor is Charging with a resistor attached to a little extra energy will be required v then \[{{U}_{\max }}\] to fall charge the Capacitor because the resistor is providing a resistance which makes less in energy in the form of heat.

The battery acts as a DC supply and as the circuit reaches the steady state that is infinite time all the voltage is seen across the capacitor as it gets fully charged and the circuit becomes circuit with no current flowing. The maximum voltage appearing across the capacitor is V making the maximum energy \[\frac{1}{2}C{{V}^{2}}\].

So, the correct answer is “Option A”.

Note:
As we know a capacitor of capacitance C and resistance R is being charged. So, be careful that a little extra energy will be required to fully charge the capacitor became less energy comes out in the form of heat. So the energy of the battery is \[\frac{1}{2}C{{V}^{2}}\]