Question

Arrange the following rational numbers in the ascending order:
\[\dfrac{7}{8},\dfrac{36}{-12},\dfrac{5}{-4},\dfrac{-2}{3}\]

Answer 1

Hint: First of all convert all fractional values into decimal numbers to visualize their magnitude. Now, draw a number line and locate all the given numbers on it. The points on the rightmost side would be the largest and as we go left, the numbers will keep on decreasing.

Complete step by step answer:
Here, we have to arrange the rational numbers: \[\dfrac{7}{8},\dfrac{36}{-12},\dfrac{5}{-4},\dfrac{-2}{3}\] in ascending order. Before proceeding with the question, let us talk about a few basic terms.
1. Ascending Order: The numbers or entities that are arranged from the smallest value to the biggest value, then that order of entities are called as ascending order. For example, 0, 2, 6, 8, 9, 11, these numbers are in ascending order.
2. Descending Order: The numbers or entities that are arranged from the biggest value to the smallest value, then that order of entities are called as descending order. For example, 11, 8, 7, 6, 2, 0, these numbers are in descending order.
3. Number Line: Number line is the pictorial representation of numbers on a straight line. It’s referring to comparing and ordering the numbers. It can be used to represent any real numbers. Zero is in the middle of the number line. All the positive numbers are at the right side of zero whereas negative numbers are at the left side of zero. As we move to the left side on it, the number decreases, whereas when we move to the right side, the number increases. For example, 1 is greater than – 2. We will represent this in the number line.

Now, let us consider our question. First of all, let us convert all the fractional values in decimal forms to visualize them. So we get,
\[\dfrac{7}{8}=0.875\]
\[\dfrac{36}{-12}=-3\]
\[\dfrac{5}{-4}=-1.25\]
\[\dfrac{-2}{3}=-0.666....7\]
Let us point all the above numbers on the number line.

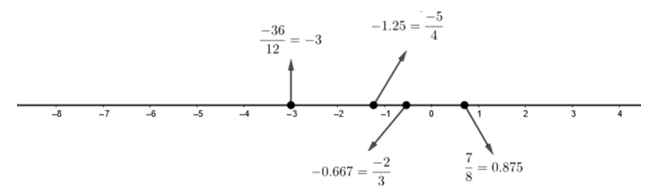
As, we know that when we go from right to left, the value of the number decreases and as we go from left to right, the value of the number increases on the number line. Hence, the smallest number among the four numbers is \[\dfrac{-36}{12}=-3\] and the largest number is \[\dfrac{7}{8}=0.875\]. So, we get the order of numbers as
\[\dfrac{-36}{12}<\dfrac{-5}{4}<\dfrac{-2}{3}<\dfrac{7}{8}\]
Therefore, we can write the given 4 numbers in ascending order as
\[\dfrac{-36}{12},\dfrac{-5}{4},\dfrac{-2}{3},\dfrac{7}{8}\]

Note: In these types of questions involving fractions, it is always better to convert them in decimal form to correctly visualize their magnitude. Also, some students get confused between ascending and descending order. So this must be very clear. Also, note that negative numbers of higher magnitude are smaller than numbers of smaller magnitude. For example, in the above solution, – 1.25 > – 3 whereas 3 > 1.25.