Question

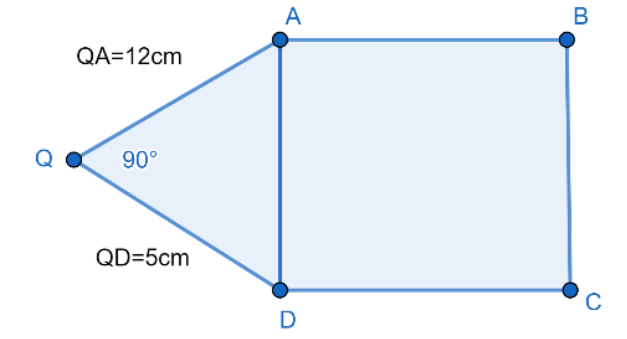
What is the area of the square ABCD shown in the diagram?

Answer 1

Hint: In this question we have to find the area of the square and for that we need the measurement of the side of the square. The triangle which is given is a right-angled triangle and measurements of its 2 sides are given. So, we can find the third side by using Pythagoras theorem. The third side of the triangle is also the side of the square.

Complete step-by-step solution:
Given: QA = 12cm
QD = 5cm
Triangle QAD is a right-angled triangle.
By using Pythagoras theorem we will find the side AD of the triangle.
${(QA)^2} + {(QD)^2} = {(AD)^2}$
$\Rightarrow {12^2} + {5^2} = A{D^2}$
$\Rightarrow 144 + 25 = A{D^2}$
$\Rightarrow A{D^2} = 169$
Squaring on both sides.
$\Rightarrow AD = \sqrt {169} $
$\Rightarrow AD = 13$cm
The formula of area of square is ${(side)^2}$. And we have found the side of square AD which is equal to 13 cm.
Area of square $ = Sid{e^2}$
$ = {13^2}$
$ = 169c{m^2}$.
So, the area of the square is $169c{m^2}$.

Note: Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides “. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle 90°.
Area of a square is defined as the number of square units needed to fill a square. In general, the area is defined as the region occupied inside the boundary of an object. The measurement is done in square units with the standard unit being square meters.