Question

What is the area of a plane figure bounded by the points of the line \[\max \left( {x,y} \right) = 1\] and \[{x^2} + {y^2} = 1\] ?

Answer 1

Hint:
Here we will first draw the line using the given information. We will find the value of the point of intersection of the curve and the given line. Then we will use integration to find the value of the required answer.

Complete step by step solution:
Here we need to find the area of a plane figure which is bounded by the points of the given line and the given curve.
By definition, \[\max \left( {x,y} \right) = 1\] means \[x = 1\] and \[y \le 1\] or \[y = 1\] and \[x \le 1\].
The given equation of the curve is \[{x^2} + {y^2} = 1\].
We can write it as \[y = \sqrt {1 - {x^2}} \]
This is the equation of the circle and the center of this circle is equal to \[\left( {0,0} \right)\] and radius is equal to 1.
Now, we will first draw the figure.

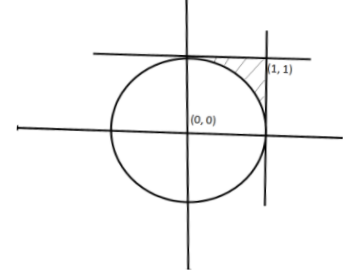
Now, we will use the integration to find the shaded area.
Required area \[ = \int\limits_0^1 {\left[ {1 - \sqrt {1 - {x^2}} } \right]} \]
Now, we will integrate each term here.
Required area \[ = \left[ x \right]_0^1 - \left[ {\dfrac{x}{2}\sqrt {1 - {x^2}} + \dfrac{1}{2}{{\sin }^{ - 1}}x} \right]_0^1\]
Now, we will put the value of the limits here.
\[ \Rightarrow \] Required area \[ = \left[ {1 - 0} \right] - \left[ {\dfrac{1}{2}\sqrt {1 - {1^2}} + \dfrac{1}{2}{{\sin }^{ - 1}}1 - \dfrac{0}{2}\sqrt {1 - {0^2}} - \dfrac{1}{2}{{\sin }^{ - 1}}0} \right]\]
Now, we will further simplify the terms here.
\[ \Rightarrow \] Required area \[ = 1 - \left[ {\dfrac{1}{2} \times 0 + \dfrac{1}{2} \times \dfrac{\pi }{2} - 0 - \dfrac{1}{2} \times 0} \right]\]
Multiplying the terms, we get
\[ \Rightarrow \]Required area \[ = 1 - \left[ {0 + \dfrac{\pi }{4} - 0} \right]\]
Now, we will open the bracket by multiplying the number \[ - 1\] to the terms.

\[ \Rightarrow \] Required area \[ = 1 - \dfrac{\pi }{4}{\rm{sq}}{\rm{.units}}\]

Note:
Here we have used the integration to find the area under the given curve. The integration function denotes the summation of data which are discrete. The integral is used to calculate the area, volume, displacement described by the function, which occurs due to a collection of small data, which cannot be measured singularly. Integration is an inverse function of differentiation. Here we have found the required area or the shaded area by finding the difference between the area under the given curve and the area under the line.