Question

Area bounded by \[y = {\sin ^{ - 1}}\left| {\sin x} \right|\] and \[y = {\left( {{{\sin }^{ - 1}}\left| {\sin x} \right|} \right)^2}\], \[0 \le x \le 2\pi \] is
A.\[\dfrac{1}{3} + \dfrac{{{\pi ^2}}}{4}\]
B.\[\dfrac{1}{6} + \dfrac{{{\pi ^3}}}{8}\]
C.\[2\]
D.None

Answer 1

Hint: Here, we will find the area bounded by the functions. We will first plot the graph of the given function. Then we will be using the concept of integration to find the area of the closed curves. Integration is the process of finding the smaller parts to find the larger area.
Formula Used: We will use the following Integration formulas:
1.\[\int {xdx = \dfrac{{{x^2}}}{2}} \]
2.\[\int {{x^2}dx = \dfrac{{{x^3}}}{3}} \]
3.Area between two curves that intersect each other in the interval \[\left[ {a,b} \right]\] is given by \[\int_a^c {\left[ {f\left( x \right) - g\left( x \right)} \right]dx + \int_c^b {\left[ {g\left( x \right) - f\left( x \right)} \right]} } dx\] where \[c\] is the root of the given two functions.

Complete step-by-step answer:
We are given that \[y = {\sin ^{ - 1}}\left| {\sin x} \right|\] and \[y = {\left( {{{\sin }^{ - 1}}\left| {\sin x} \right|} \right)^2}\], \[0 \le x \le 2\pi \]
Let \[f\left( x \right) = {\sin ^{ - 1}}\left| {\sin x} \right|\] and \[g\left( x \right) = {\left( {{{\sin }^{ - 1}}\left| {\sin x} \right|} \right)^2}\].
We will first plot the graph for the trigonometric function.
     

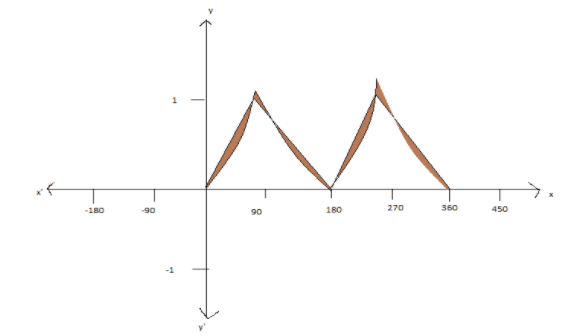
We know that,
\[{\sin ^{ - 1}}\left| {\sin x} \right| = x\] when \[0 \le x \le \dfrac{\pi }{2}\]
\[{\sin ^{ - 1}}\left| {\sin x} \right| = \pi - x\] when \[\dfrac{\pi }{2} \le x \le \pi \]
\[{\sin ^{ - 1}}\left| {\sin x} \right| = - \pi + x\] when \[\pi \le x \le \dfrac{{3\pi }}{2}\]
\[{\sin ^{ - 1}}\left| {\sin x} \right| = 2\pi - x\] when \[\dfrac{{3\pi }}{2} \le x \le 2\pi \]
We know that \[\sin x\] always lies between 0 and 1.
From the graph, \[\left( {1,1} \right)\] is the point of intersection of the given two curves.
Area between two curves that intersect each other in the interval \[\left[ {a,b} \right]\] is given by \[\int_a^c {\left[ {f\left( x \right) - g\left( x \right)} \right]dx + \int_c^b {\left[ {g\left( x \right) - f\left( x \right)} \right]} } dx\] where \[c\] is the root of the given two functions.
From the graph the function is symmetrical and substituting \[{\sin ^{ - 1}}\left| {\sin x} \right| = x\] we get
Area of the bounded region \[ = 4\left[ {\int\limits_0^1 {x - {x^2}dx} + \int\limits_1^{\dfrac{\pi }{2}} {{x^2} - xdx} } \right]\]
By using the integration formula, \[\int {xdx = \dfrac{{{x^2}}}{2}} \], \[\int {{x^2}dx = \dfrac{{{x^3}}}{3}} \] we get
\[ \Rightarrow \] Area of the bounded region \[ = 4\left[ {\left[ {\dfrac{{{x^2}}}{2} - \dfrac{{{x^3}}}{3}} \right]_0^1 + \left[ {\dfrac{{{x^3}}}{3} - \dfrac{{{x^2}}}{2}} \right]_1^{\dfrac{\pi }{2}}} \right]\]
Now, by substituting the upper limit and lower limit, we get
\[ \Rightarrow \] Area of the bounded region \[ = 4\left[ {\left[ {\left( {\dfrac{{{1^2}}}{2} - \dfrac{{{1^3}}}{3}} \right) - 0} \right] + \left[ {\left( {\dfrac{{{\pi ^3}}}{{{2^3} \cdot 3}} - \dfrac{{{\pi ^2}}}{{{2^2} \cdot 2}}} \right) - \left( {\dfrac{{{1^3}}}{3} - \dfrac{{{1^2}}}{2}} \right)} \right]} \right]\]
\[ \Rightarrow \] Area of the bounded region \[ = 4\left[ {\dfrac{2}{2} - \dfrac{2}{3} + \dfrac{{{\pi ^3}}}{{24}} - \dfrac{{{\pi ^2}}}{8}} \right]\]
By simplifying the equation, we get
\[ \Rightarrow \] Area of the bounded region \[ = 4\left[ {1 - \dfrac{2}{3} + \dfrac{{{\pi ^3}}}{{24}} - \dfrac{{{\pi ^2}}}{8}} \right]\]
\[ \Rightarrow \] Area of the bounded region \[ = 4\left[ {1 \times \dfrac{3}{3} - \dfrac{2}{3} + \dfrac{{{\pi ^3}}}{{24}} - \dfrac{{{\pi ^2}}}{8}} \right]\]
Multiplying and subtracting the terms, we get
\[ \Rightarrow \] Area of the bounded region \[ = 4\left[ {\dfrac{1}{3} + \dfrac{{{\pi ^3}}}{{24}} - \dfrac{{{\pi ^2}}}{8}} \right]\]
\[ \Rightarrow \] Area of the bounded region \[ = \left[ {\dfrac{4}{3} + \dfrac{{4{\pi ^3}}}{{24}} - \dfrac{{4{\pi ^2}}}{8}} \right]\]
By dividing the equation, we get
\[ \Rightarrow \] Area of the bounded region \[ = \left[ {\dfrac{4}{3} + \dfrac{{{\pi ^3}}}{6} - \dfrac{{{\pi ^2}}}{2}} \right]\]
\[ \Rightarrow \] Area of the bounded region \[ = \left[ {\dfrac{4}{3} + \left( {\dfrac{{{\pi ^3}}}{6} - \dfrac{{{\pi ^2}}}{2}} \right)} \right]\]
Therefore, the area of the bounded region is \[\left[ {\dfrac{4}{3} + \left( {\dfrac{{{\pi ^3}}}{6} - \dfrac{{{\pi ^2}}}{2}} \right)} \right]\].
Thus Option(A) is the correct answer.

Note: We need to know that the trigonometric functions are always symmetrical to each other. We know that sine and the inverse of sine always lies between 0 and 1. Whenever there is an intersection of two functions, then the area of the curve is found by subtracting the function of the lower curve from the function of the upper curve. We should also remember that the lower limit has to be subtracted from the upper limit.