Question

What are the oxidation numbers of the underlined elements in each of the following and how do you rationalize your result?
a. \[K{\underline I _3}\]
b. ${H_2}{\underline S _4}{O_6}$
c. ${\underline {Fe} _3}{O_4}$
d. $\underline C {H_3}\underline C {H_2}OH$
e. $\underline C {H_3}\underline C OOH$

Answer 1

Hint: In simple words, the oxidation number is the number assigned to the components in a chemical combination. The oxidation number is the total number of electrons that atoms in a molecule can share, lose, or gain while forming chemical interactions with atoms of another element.

Complete answer:
(a) \[K{\underline I _3}\]
The oxidation number (O.N.) of \[K\] in \[K{I_3}\] is \[ + 1\] . As a result, average oxidation number of $I$ is $ - \dfrac{1}{3}$ . O.N., on the other hand, cannot be fractional. To determine the oxidation states, we must first consider the structure of \[K{I_3}\] . An iodine atom forms a coordinate covalent bond with an iodine molecule in a \[K{I_3}\] molecule.
\[\mathop {{K^ + }}\limits^{ + 1} {\left[ {\mathop I\limits^0 - \mathop {I\,}\limits^0 \leftarrow \mathop I\limits^{ - 1} } \right]^ - }\]
As a result, the O.N. of the two \[I\] atoms that make up the \[{I_2}\] molecule in a \[K{I_3}\] molecule is \[0\], whereas the O.N. of the \[I\] atom that makes up the coordinate bond is \[-1.\]
(b) ${H_2}{\underline S _4}{O_6}$
 ${\mathop H\limits^{ + 1} _2}\mathop S\limits^x {O_4}{\mathop O\limits^{ - 2} _6}$
Now,
$
  2\left( { + 1} \right) + 4\left( x \right) + 6\left( { - 2} \right) = 0 \\
   \Rightarrow 2 + 4x - 12 = 0 \\
   \Rightarrow x = + 2\dfrac{1}{2} \\
 $
O.N., on the other hand, cannot be fractional. As a result, \[S\] in the molecule must exist in several oxidation states.

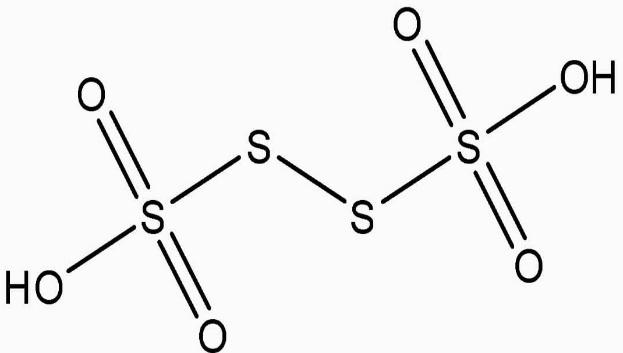
Two of the four S atoms have an O.N. of +5, whereas the other two have an O.N. of 0.
c. ${\underline {Fe} _3}{O_4}$
The O.N. of \[Fe\] is determined to be when the O.N. of \[O\] is set to \[-2\] . \[{}^{ + 2}\left( {\dfrac{2}{3}} \right)\] O.N., on the other hand, cannot be fractional.
One of the three \[Fe\] atoms in this example has an O.N. of \[ + 2\] , whereas the other two \[Fe\] atoms have an O.N. of \[ + 3\] .
$\mathop {Fe}\limits^{ + 2} O,\mathop {Fe}\limits^{ + 3} {O_3}$
d. $\underline C {H_3}\underline C {H_2}OH$
${\mathop C\limits^x _2}{\mathop H\limits^{ + 1} _6}{\mathop O\limits^{ - 2} _2}$
\[
  2\left( x \right) + 4\left( { + 1} \right) + 2\left( { - 2} \right) = 0 \\
   \Rightarrow 2x + 4 - 4 = 0 \\
   \Rightarrow x = 0 \\
 \]
Hence, the O.N of \[C\] is \[-2\] .
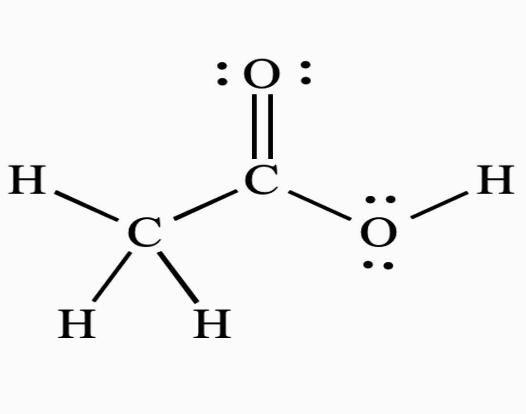
e. $\underline C {H_3}\underline C OOH$
${\mathop C\limits^x _2}{\mathop H\limits^{ + 1} _4}{\mathop O\limits^{ - 2} _2}$
$
  2\left( x \right) + 4\left( { + 1} \right) + 2\left( { - 2} \right) = 0 \\
   \Rightarrow 2x + 4 - 4 = 0 \\
   \Rightarrow x = 0 \\
 $
The average O.N. of \[C\] , on the other hand, is \[0\]. This molecule's two carbon atoms are found in two separate settings. As a result, their oxidation numbers cannot be the same. As a result, \[C\]in \[C{H_3}COOH\] has the oxidation states \[ + 2\] and \[ - 2\]

Note:
A negative oxidation state is attributed to the more electronegative element in a material. A positive oxidation state is attributed to the less electronegative element. Keep in mind that electronegativity is highest at the top-right corner of the periodic table and falls toward the bottom-left corner.