Question

What are the first 100 digits of $\pi $ ?

Answer 1

Hint: $\pi $ is a non-repeating non-terminating irrational number. For calculation purposes we just need the value 3.141 but $\pi $ has been a very attractive number for mathematicians for many decades. Currently, the best method we have to find its value is by using the Binomial theorem.

Complete step by step solution:
The very first attempts to calculate the value of $\pi $ were made by drawing a hexagon inside the circle, and a square outside the circle. This was just sufficient to tell us that $3<\pi <4$ .
This hexagon was further bisected into the dodecagon (12 sides) to get a more precise value. This process was repeated for many years.
Then, amidst a pandemic, came the ground-breaking work of famous mathematician and physicist Sir Isaac Newton.
He used Binomial theorem to calculate $\pi $ . This is how he did it.
We know that according to Binomial theorem,
$\begin{align}
  & {{\left( x+y \right)}^{n}}=\sum\limits_{r=0}^{n}{{}^{n}{{C}_{r}}{{x}^{n-r}}{{y}^{r}}} \\
 & \text{where }n\in N\text{ and }x,y\in R. \\
\end{align}$
The expansion of this Binomial theorem for any index n, such that, n is a rational number, x is a real number and |x| < 1, gives the following result
${{\left( 1+x \right)}^{n}}=1+nx+\dfrac{n\left( n-1 \right)}{2!}{{x}^{2}}+\dfrac{n\left( n-1 \right)\left( n-2 \right)}{3!}{{x}^{3}}+...+\dfrac{n\left( n-1 \right)\left( n-2 \right)...\left( n-r-1 \right)}{r!}{{x}^{r}}+...\infty $
For $n=\dfrac{1}{2}$ , we have
${{\left( 1+x \right)}^{\dfrac{1}{2}}}=1+\dfrac{1}{2}x+\dfrac{\dfrac{1}{2}\left( \dfrac{1}{2}-1 \right)}{2!}{{x}^{2}}+\dfrac{\dfrac{1}{2}\left( \dfrac{1}{2}-1 \right)\left( \dfrac{1}{2}-2 \right)}{3!}{{x}^{3}}+...+\dfrac{\dfrac{1}{2}\left( \dfrac{1}{2}-1 \right)\left( \dfrac{1}{2}-2 \right)...\left( \dfrac{1}{2}-r-1 \right)}{r!}{{x}^{r}}+...\infty $
\[\Rightarrow {{\left( 1+x \right)}^{\dfrac{1}{2}}}=1+\dfrac{1}{2}x-\dfrac{1}{8}{{x}^{2}}+\dfrac{1}{16}{{x}^{3}}-\dfrac{5}{128}{{x}^{4}}+...\infty \text{ }...\left( i \right)\]
Let us assume a unit circle with centre at (0,0). Equation of this circle is ${{x}^{2}}+{{y}^{2}}=1$ . We can solve this equation further as,
${{y}^{2}}=1-{{x}^{2}}$
For positive values of y, we have
$y=\sqrt{1-{{x}^{2}}}$
We can expand the RHS using equation (i) to get
$y=1-\dfrac{1}{2}{{x}^{2}}-\dfrac{1}{8}{{x}^{4}}-\dfrac{1}{16}{{x}^{6}}-\dfrac{5}{128}{{x}^{8}}+...\infty $

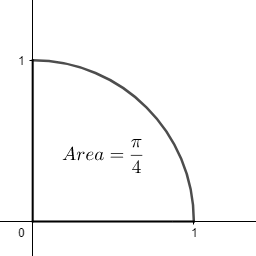
If we now integrate y from 0 to 1, we get the following area,
Thus, we can write,
$\int\limits_{x=0}^{x=1}{ydx}=\int\limits_{x=0}^{x=1}{\left( 1-\dfrac{1}{2}{{x}^{2}}-\dfrac{1}{8}{{x}^{4}}-\dfrac{1}{16}{{x}^{6}}-\dfrac{5}{128}{{x}^{8}}+...\infty \right)}dx$
$\Rightarrow \dfrac{\pi }{4}=\left( x-\dfrac{1}{2}\dfrac{{{x}^{3}}}{3}-\dfrac{1}{8}\dfrac{{{x}^{5}}}{5}-\dfrac{1}{16}\dfrac{{{x}^{7}}}{7}-\dfrac{5}{128}\dfrac{{{x}^{9}}}{9}+...\infty \right)_{x=0}^{x=1}$
$\Rightarrow \dfrac{\pi }{4}=\left( 1-\dfrac{1}{6}-\dfrac{1}{40}-\dfrac{1}{112}-\dfrac{5}{1152}-...\infty \right)$
$\Rightarrow \pi =4\left( 1-\dfrac{1}{6}-\dfrac{1}{40}-\dfrac{1}{112}-\dfrac{5}{1152}-...\infty \right)$
We can use this arithmetic expression to evaluate the value of $\pi $ with great precision.
We need the first 100 digits of $\pi $ , which will take at least a few days for us to solve. But ultimately, we can get our value of $\pi $ with hundred digits, and it will look exactly like this,
$\begin{align}
  & \pi =3.1415926535\text{ }8979323846\text{ }2643383279\text{ }5028841971\text{ }6939937510\text{ } \\
 & 5820974944\text{ }5923078164\text{ }0628620899\text{ }8628034825\text{ }342117067 \\
\end{align}$

Note: We must remember that $\pi $ is a non-repeating non-terminating irrational number. Therefore, it is impossible to list, or even find all digits of the number $\pi $ . We must not ignore the fact that the traditional Binomial theorem is applicable only when n is a natural number.