Question

What are Skew lines? Do they lie in the same plane?

Answer 1

Hint: In order to understand what skew lines are one first needs to understand the terms such as parallel lines, coplanar lines, intersecting lines.
Parallel lines: Lines that lie on the same plane but never meet each other are called parallel lines.
Coplanar lines: Those lines that lie on the same plane are called coplanar lines.
Intersecting lines: Those lines that lie on the same plane and meet each other are called intersecting lines.

Complete step by step answer:

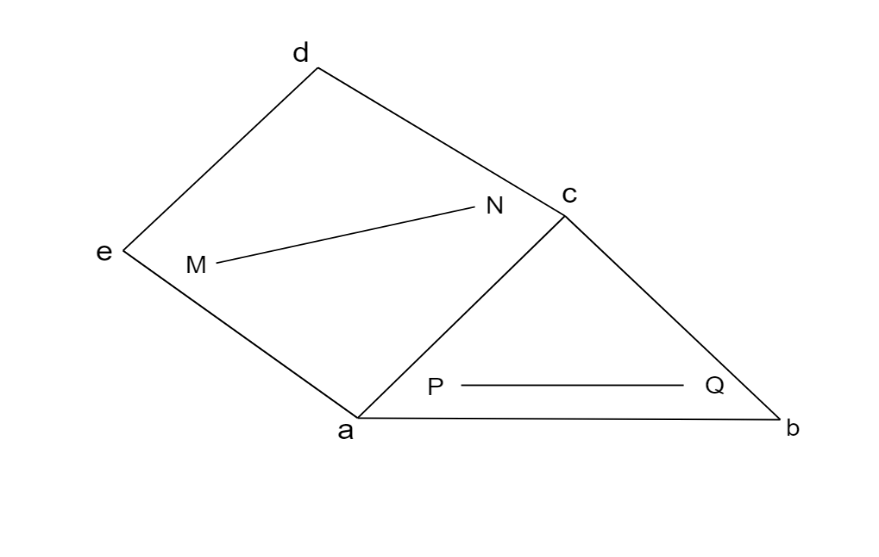
Two or more lines that are non-intersecting, neither parallel to each other nor coplanar with respect to each other are called skew lines. For example, the lines MN and PQ shown in the figure are skew lines.
Since these are not coplanar, this means that these lines do not lie in the same plane.
Skew lines can be found in three or more dimensions.
Examples of skew lines:
a) the lines drawn on the ceiling surface and the walls are Skew lines to each other. Because the lines drawn on these surfaces are in different planes so they will never intersect each other and also will not be parallel to each other.
b) roads along highways and flyover in the cities: since the roads are in different planes the lines found on these roads will never intersect each other nor they be parallel to each other.

Note:
One major difficulty students face is that they can’t decide whether skew lines are perpendicular or not. Skew lines can never be perpendicular to each other. Perpendicular lines are the lines that intersect each other at right angles, and we know that skew lines are non-intersecting lines so the skew lines can never become perpendicular to each other.