Question

What is the angle subtended by an edge of a regular tetrahedron at its centre?
(a) \[{{\cos }^{-1}}\left( \dfrac{-1}{2} \right)\]
(b) \[{{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{2}} \right)\]
(c) \[{{\cos }^{-1}}\left( \dfrac{-1}{3} \right)\]
(d) \[{{\cos }^{-1}}\left( \dfrac{-1}{\sqrt{3}} \right)\]

Answer 1

Hint: In this question, we first need to draw the diagram of the tetrahedron formed by joining the unit vectors \[\vec{a},\vec{b},\vec{c}\] . Now, as we know the angle between two of these vectors we get the dot product of them using the formula \[\vec{a}\cdot \vec{b}=\left| {\vec{a}} \right|\left| {\vec{b}} \right|\cos \theta \]. Then find the centre and then again find the angle subtended by an edge at centre using the formula \[\cos \theta =\dfrac{\overrightarrow{AP}\cdot \overrightarrow{BP}}{\left| \overrightarrow{AP} \right|\left| \overrightarrow{BP} \right|}\]

Complete step-by-step solution -
A regular tetrahedron is a tetrahedron in which all four faces are equilateral triangles.
Now, let us draw the diagram of tetrahedron joining the vectors \[\vec{a},\vec{b},\vec{c}\]

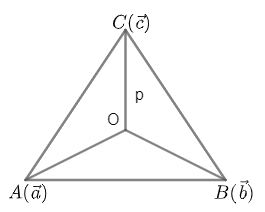
Now, here \[\vec{a},\vec{b},\vec{c}\] are unit vectors which means that
\[\Rightarrow \left| {\vec{a}} \right|=\left| {\vec{b}} \right|=\left| {\vec{c}} \right|=1\]
Now, as they form equilateral triangles as it is a regular tetrahedron we have the angles between
\[\vec{a},\vec{b}=\vec{b},\vec{c}=\vec{c},\vec{a}=\dfrac{\pi }{3}\]
Now, let us calculate the dot products of respective vectors using the formula
\[\vec{a}\cdot \vec{b}=\left| {\vec{a}} \right|\left| {\vec{b}} \right|\cos \theta \]
Now, on substituting the respective values we get,
\[\therefore \vec{a}\cdot \vec{b}=\dfrac{1}{2}\text{ }\left[ \because \cos \dfrac{\pi }{3}=\dfrac{1}{2} \right]\]
Now, from the above conditions we get,
\[\Rightarrow \vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{c}=\vec{c}\cdot \vec{a}=\dfrac{1}{2}\]
Now, let us find the centre of the tetrahedron
\[p=\dfrac{\vec{o}+\vec{a}+\vec{b}+\vec{c}}{4}\]
Now, we need to find the angle between \[\overrightarrow{AP}\]& \[\overrightarrow{BP}\]
\[\Rightarrow \cos \theta =\dfrac{\overrightarrow{AP}\cdot \overrightarrow{BP}}{\left| \overrightarrow{AP} \right|\left| \overrightarrow{BP} \right|}\]
Let us now substitute the respective vector values in the above formula
\[\Rightarrow \cos \theta =\dfrac{\left( \dfrac{\vec{a}+\vec{b}+\vec{c}}{4}-\vec{a} \right)\cdot \left( \dfrac{\vec{a}+\vec{b}+\vec{c}}{4}-\vec{b} \right)}{\left| \dfrac{\vec{a}+\vec{b}+\vec{c}}{4}-\vec{a} \right|\left| \dfrac{\vec{a}+\vec{b}+\vec{c}}{4}-\vec{b} \right|}\]
Now, on further simplification of the respective terms we get,
\[\Rightarrow \cos \theta =\dfrac{\left( \vec{b}+\vec{c}-3\vec{a} \right)\cdot \left( \vec{a}+\vec{c}-3\vec{b} \right)}{\left| \vec{b}+\vec{c}-3\vec{a} \right|\left| \vec{a}+\vec{c}-3\vec{b} \right|}\]
Now, on doing the respective dot products and simplifying further we get,
Here, the magnitude of the vectors in the denominator will be same as the vectors have the same magnitude.
\[\Rightarrow \cos \theta =\dfrac{\vec{a}\cdot \vec{b}+\vec{b}\cdot \vec{c}-3{{{\vec{b}}}^{2}}+\vec{c}\cdot \vec{a}+{{{\vec{c}}}^{2}}-3\vec{b}\cdot \vec{c}-3{{{\vec{a}}}^{2}}-3\vec{c}\cdot \vec{a}+9\vec{a}\cdot \vec{b}}{{{{\vec{b}}}^{2}}+{{{\vec{c}}}^{2}}+9{{{\vec{a}}}^{2}}+2\vec{b}\cdot \vec{c}-6\vec{c}\cdot \vec{a}-6\vec{a}\cdot \vec{b}}\]
Let us now substitute the respective values to simplify further
\[\Rightarrow \cos \theta =\dfrac{\dfrac{1}{2}+\dfrac{1}{2}-3+\dfrac{1}{2}+1-\dfrac{3}{2}-3-\dfrac{3}{2}+\dfrac{9}{2}}{1+1+9+\dfrac{2}{2}-\dfrac{6}{2}-\dfrac{6}{2}}\]
Now, on simplifying it further we get,
\[\Rightarrow \cos \theta =\dfrac{-5+3}{6}\]
Now, this can be further written as
\[\Rightarrow \cos \theta =\dfrac{-2}{6}\]
\[\Rightarrow \cos \theta =\dfrac{-1}{3}\]
Now, on taking the cosine function to other side to get the value of angle we get,
\[\therefore \theta ={{\cos }^{-1}}\left( \dfrac{-1}{3} \right)\]
Hence, the correct option is (c).

Note: Instead of using the vectors \[\overrightarrow{AP},\overrightarrow{BP}\] we can also use the other one with any of these and simplify by substituting in the same formula and then solve accordingly to get the result. Both the methods give the same result as it is a regular tetrahedron.
It is important to note that we need to find the dot product first as we already know the respective angles. It is also to be noted that while substituting and simplifying we need to cross check the terms and the signs as there is a lot of possibility for making a mistake.