
Angle between p-orbitals is:
A.${{90}^{0}}$
B.${{180}^{0}}$
C.${{120}^{0}}$
D.${{109}^{0}}28'$
Answer
567k+ views
Hint: The p orbitals are placed in such a way that electronic repulsion is minimized. The lobes at the front face away from each other, forming a straight line. P-orbitals are generally dumb-bell shaped.
Complete step-by step solution:
-In order to answer our question, let us know some facts about the p-orbitals.
-Shape: For p-orbitals, l=1, so there are three possible orientations as m= -1/0/1. This means that there are three p-orbitals whose axes are mutually perpendicular. These are designated as ${{p}_{x}},{{p}_{y}},{{p}_{z}}$ in each p subshells. The three orbitals are equal in size, shape and energy, but their orientation is different.
-Size and energy: P-orbitals increase in size and energy with the increase in principal quantum number. The order is: $4p>3p>2p$
Nodes:
-Radial nodes: Radial nodes are circular rings that occur as the principal quantum number increases. Here, the number of radial nodes for p orbitals is given by (n-2) formula. Thus there is no radial node in 2p orbital or number of radial nodes also calculated by the formula= n-l-1.
-Angular nodes: Angular nodes represent the plane/ planes that pass through the nucleus, or the origin where the probability density is equal to zero. Angular nodes number is equal to the value of ‘l’.
Following are the three p-orbitals:
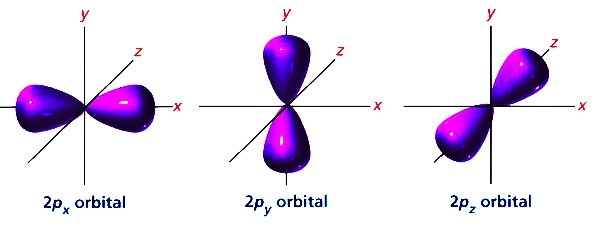
So, we can clearly see from the diagram that the orbitals are aligned according to their respective axes. Since the x,y and z axes are aligned perpendicular to each other, so two p-orbitals are also aligned perpendicular to each other.
So, we get our answer as option A.
NOTE: Following is the table which gives an idea about the number of nodes in p orbital:
Complete step-by step solution:
-In order to answer our question, let us know some facts about the p-orbitals.
-Shape: For p-orbitals, l=1, so there are three possible orientations as m= -1/0/1. This means that there are three p-orbitals whose axes are mutually perpendicular. These are designated as ${{p}_{x}},{{p}_{y}},{{p}_{z}}$ in each p subshells. The three orbitals are equal in size, shape and energy, but their orientation is different.
-Size and energy: P-orbitals increase in size and energy with the increase in principal quantum number. The order is: $4p>3p>2p$
Nodes:
-Radial nodes: Radial nodes are circular rings that occur as the principal quantum number increases. Here, the number of radial nodes for p orbitals is given by (n-2) formula. Thus there is no radial node in 2p orbital or number of radial nodes also calculated by the formula= n-l-1.
-Angular nodes: Angular nodes represent the plane/ planes that pass through the nucleus, or the origin where the probability density is equal to zero. Angular nodes number is equal to the value of ‘l’.
Following are the three p-orbitals:

So, we can clearly see from the diagram that the orbitals are aligned according to their respective axes. Since the x,y and z axes are aligned perpendicular to each other, so two p-orbitals are also aligned perpendicular to each other.
So, we get our answer as option A.
NOTE: Following is the table which gives an idea about the number of nodes in p orbital:
| Orbital | Radial nodes |
| 2p | 0 |
| 3p | 1 |
| 4p | 2. |
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




