Question

What is the angle between minute hand and hour hand at 2o’clock?

Answer 1

Hint: We will first draw the clock diagram with proper labelling and then we will try to find out the angle between two consecutive digits in the clock. Then by using the unitary method we will find the angle between minute hand and hour hand at 2o'clock.

Complete step-by-step answer:
It is given in the question that we have to find out the angle between minutes hand and hour hand at time 2o'clock. We will find the angle between minute hand and hour hand by using the unitary method.
So, the unitary method is a technique for solving a problem by first finding the value of a single unit and then finding the required value by multiplying the single unit value. This mathematical approach is also used to find the value of a unit from the value of multiple units.

The below diagram is showing a clock.

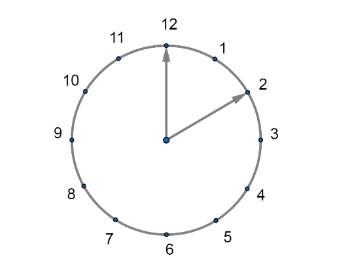
We know that a complete circle is of $360{}^\circ $ and so is it in a clock of 12 hours. We have 12 equal parts of each same angle.
So, using the unitary method we can find the angle of each part. We know that the complete circle has $360{}^\circ $ and there are 12 equal parts in a clock. So, angle of each part can be calculated as,
$\begin{align}
  & =\dfrac{total\ angle}{parts} \\
 & =\dfrac{360{}^\circ }{12} \\
 & =30{}^\circ \\
\end{align}$
Thus, the angle between two consecutive numbers or 1 part is $30{}^\circ $.
Now, we will look at the clock to find the angle between minute hand and hour hand at 2o'clock. As from the diagram of the clock, we can see that there are two parts which are covered between the minute hand which is at 12 and hour hand which is at 2.
So, using unitary method we can find angle between two consecutive numbers in clock,
$\begin{align}
  & =2\times one\ part \\
 & =2\times 30{}^\circ \\
 & =60{}^\circ \\
\end{align}$
Thus, the angle between the clock hand and minute hand at 2o'clock will be $60{}^\circ $.

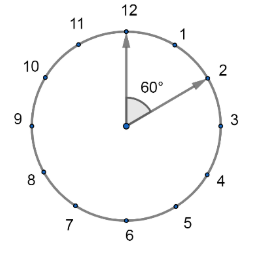
Note: Always remember that the angle between two consecutive numbers in a clock of 12 hour is always $30{}^\circ $. This will save our time while solving questions based on the clock. If the clock is of 24 hour, then we can find the angle between two consecutive numbers using the unitary method as $\dfrac{360{}^\circ }{24}$. We get $15{}^\circ $ as the result when the clock is a 24 hour clock.