Question

: Analyse the given graph, drawn between concentrations of reactants vs. time.

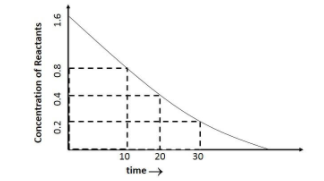
A.Predict the order of the reaction.
B.Theoretically, can the concentration of the reactant reduce to zero after infinite time? Explain.

Answer 1

Hint: In the above diagram, the concentration of the reactant decrease exponentially with time. Hence, the rate of the reaction is determined by the concentration of the reactants.
Formula Used:
The first order rate equation, ${\text{A = }}{{\text{A}}_{\text{0}}}{\text{ }}{{\text{e}}^{{\text{ - kt}}}}$
$ \Rightarrow {{\text{A}}_{\text{0}}}{\text{ = A }}{{\text{e}}^{{\text{kt}}}}$
where, A is the concentration of the reactant at time t and ${{\text{A}}_{\text{0}}}$is the initial concentration of the reactant.

Complete step by step answer:
Coming to the first part of the question, it can be seen that, the concentration of the reactant decreases exponentially with time which is a characteristic of the “First-Order Reaction” and the rate of the reaction here is proportional to the first power of the concentration of the reactants.
From the graph it can be seen that,
At time, t = 10, C = $0.8$
At t = 20, C = $0.4$
At t = 30, C = $0.2$, putting the values in the first order rate equation we have:
${{\text{A}}_{\text{0}}}{\text{ = 0}}{\text{.8 }}{{\text{e}}^{10{\text{k}}}}$..................... (1)
${{\text{A}}_{\text{0}}}{\text{ = 0}}{\text{.4 }}{{\text{e}}^{20{\text{k}}}}$..................... (2)
${{\text{A}}_{\text{0}}}{\text{ = 0}}{\text{.2 }}{{\text{e}}^{30{\text{k}}}}$..................... (3)
Comparing equation (1) and (2) we get,
${\text{0}}{\text{.4 }}{{\text{e}}^{20{\text{k}}}}{\text{ = 0}}{\text{.8 }}{{\text{e}}^{10{\text{k}}}}$
$ \Rightarrow \dfrac{{0.8}}{{0.4}} = {e^{20k - 10k}}$
Solving this:
$ \Rightarrow {e^{{\text{10k}}}} = 2$
Taking log on both sides of the equation we get,
$\ln 2 = {\ln _e}{e^{10{\text{k}}}} \Rightarrow 0.693 = 10{\text{k}}$
$ \Rightarrow {\text{k}} = 0.0693{\text{ se}}{{\text{c}}^{ - 1}}$
Again comparing equation (2) and (3) we get,
${\text{0}}{\text{.4 }}{{\text{e}}^{20{\text{k}}}}{\text{ = 0}}{\text{.2 }}{{\text{e}}^{30{\text{k}}}}$
\[ \Rightarrow \dfrac{{0.4}}{{0.2}} = {e^{30k - 20k}}\]
Solving this:
$ \Rightarrow {e^{{\text{10k}}}} = 2$
Taking log on both sides of the equation we get,
$\ln 2 = {\ln _e}{e^{10{\text{k}}}} \Rightarrow 0.693 = 10{\text{k}}$
$ \Rightarrow {\text{k}} = 0.0693{\text{ se}}{{\text{c}}^{ - 1}}$
As, in both eases we get the same values of rate constants, so the reaction satisfies “First Order Condition”
Coming to the second part of the question, putting the value A = 0 in the above equation, we get,
${\text{ }}{{\text{A}}_{\text{0}}}{\text{ }}{{\text{e}}^{{\text{ - kt}}}} = 0$, therefore, ${\text{ }}{{\text{e}}^{{\text{ - kt}}}} = 0$
Hence, ${\text{t}} = \infty $ , since k cannot be zero. So, theoretically, the concentration of the reactant will become 0 at infinite time.

Note:
The order of the reaction can be defined as the sum of the powers of the concentration of the reactants in the rate law expression. For first order reactions, the half-life is independent of the initial and final concentration of the reactants and is dependent on the rate constant of the reaction and can be written as:
${t_{1/2}} = \dfrac{{0.693}}{{\text{k}}}$ where k is the rate constant.