Question

An unstable heavy nucleus at rest breaks into two nuclei which move away with velocities in the ratio of 8: 27. The ratio of the radii of the nuclei (assumed to be spherical) is:

A. \[8:27\]
B. \[2:3\]
C. \[3:2\]
D. \[4:9\]

Answer 1

Hint: From the ratio of the velocities, we will be able to determine the ratio of their atomic masses by using the momentum conservation theorem. Next, using the formula for the radius of a nuclei, we will be able to find the ratio of their radii.

Formula Used: Momentum conservation theorem: ${m_1}{v_1} = {m_2}{v_2}$
Where ${m_1},{m_2}$ are the masses of the fission nuclei and is expressed in kilograms $(kg)$ and ${v_1},{v_2}$ are their velocities and is expressed in meter per second $(m/s)$.

Radius of a nuclei: $r = {r_0}{A^{1/3}}$
Where $r$ is the radius of the nuclei and is expressed in meters $(m)$. It is represented as ${r_1},{r_2}$ for the two nuclei.${r_0}$ is a constant and is equal to $1.2fm$. $A$ is the atomic masses of the fission nuclei and is expressed in kilograms $(kg)$. It is represented as ${A_1},{A_2}$ for the two nuclei.

Complete step by step answer:When an unstable nuclei fissions, it breaks into two nuclei which move away at a particular velocity like shown below:

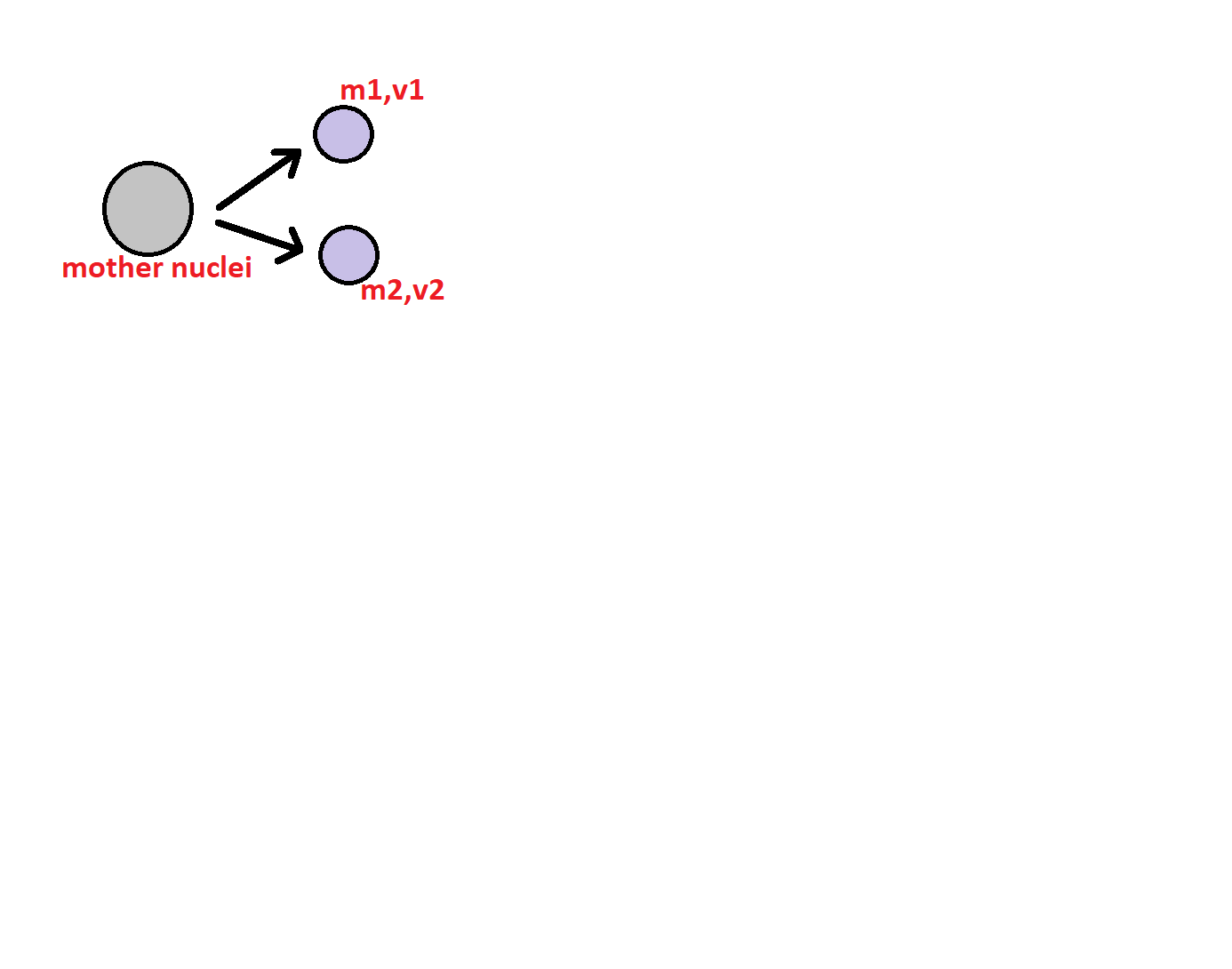
This system has conservation of momentum at all points. Therefore we can say that ${m_1}{v_1} = {m_2}{v_2}$.
Upon rearrangement we get,
$
  {m_1}{v_1} = {m_2}{v_2} \\
   \Rightarrow \dfrac{{{m_1}}}{{{m_2}}} = \dfrac{{{v_2}}}{{{v_1}}} \\
 $
Substituting the values we get,
$
  \dfrac{{{m_1}}}{{{m_2}}} = \dfrac{{{v_2}}}{{{v_1}}} = \dfrac{{27}}{8} \\
   \Rightarrow \dfrac{{{m_1}}}{{{m_2}}} = \dfrac{{27}}{8} \\
 $
For nuclei, mass will be represented using $A$ instead of $m$. Making this substitution we get,
$
  \dfrac{{{m_1}}}{{{m_2}}} = \dfrac{{27}}{8} = \dfrac{{{A_1}}}{{{A_2}}} \\
   \Rightarrow \dfrac{{{A_1}}}{{{A_2}}} = \dfrac{{27}}{8} \\
 $
Now, we know that $r = {r_0}{A^{1/3}}$.
Taking this formula for each nuclei we get,
${r_1} = {r_0}{A_1}^{1/3}$ and ${r_2} = {r_0}{A_2}^{1/3}$.
Dividing these two we get,
$\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{{{A_1}^{1/3}}}{{{A_2}^{1/3}}}$
Substituting the values of ${A_1},{A_2}$ in this to get a ratio of their radii $r$,
$
  \dfrac{{{r_1}}}{{{r_2}}} = \dfrac{{{A_1}^{1/3}}}{{{A_2}^{1/3}}} = \dfrac{{{{27}^{1/3}}}}{{{8^{1/3}}}} \\
   \Rightarrow \dfrac{{{r_1}}}{{{r_2}}} = \dfrac{3}{2} \\
 $
Therefore, the ratio of their radii is $3:2$.
In conclusion, the correct option is C.

Note:It is interesting to see the law of conservation of momentum of classical physics being applied in quantum physics. This was assumed as a case of general two bodies in motion and therefore the law helped us solve it easily.