Question

An open box with a square base is to be made out of a given quantity of cardboard of area $ {c^2} $ . Show that the maximum volume of the box is $ \dfrac{{{c^3}}}{{6\sqrt 3 }} $ .

Answer 1

Hint: We know that open box is in the form of cuboid ,we will use the expression of volume of cuboid and lateral surface area. We assume the sides of the open box as base is given as square shaped . Then we will find the expression of height from the expression of area. We will substitute this in expression of volume. We will then differentiate volume with respect to $ x $ to find the value of $ x $ . We will again differentiate volume to check for maxima and minima. Then we will finally substitute the value of height and sides in the expression of volume to prove the result given in question.

Complete step-by-step answer:

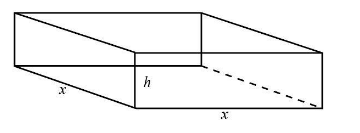
Since the box is having a square base. Let us assume the length and breadth of the square base as $ x $ . This can be expressed as
 $ l = x $ and $ b = x $
Let us assume the height of the open box as $ h $ .
We know that the expression for volume of open box which is in the shape of cuboid is
 $ V = lbh $
We will substitute $ x $ for $ l $ , $ x $ for $ b $ and $ h $ for $ h $ in the above expression.
 $ \begin{array}{c}
V = x \cdot x \cdot h\\
V = {x^2}h
\end{array} $ ……(i)
We know that surface of the open box can be expressed as:
 $ {\rm{Surface \; area \; of \; open \; box}} = lb + 4bh $
We will substitute $ x $ for $ l $ , $ x $ for $ b $ and $ h $ for $ h $ in the above expression, we will get,
 $ \begin{array}{l}
{\rm{Surface \; area \; of \; open \; box}} = \left( {x \cdot x} \right) + 4\left( {h \cdot x} \right)\\
{\rm{Surface \; area \; of \; open \; box}} = {x^2} + 4hx
\end{array} $
But surface area of the open box is given as $ {c^2} $ in the question, hence we will substitute $ {c^2} $ for surface area in the above expression, we will get,
 $ {c^2} = {x^2} + 4hx $
We will find the value of $ h $ from the above expression,
 $ \begin{array}{c}
4hx = {c^2} - {x^2}\\
h = \dfrac{{{c^2} - {x^2}}}{{4x}}
\end{array} $ ……(ii)
 We will substitute the value of $ h $ in the equation (i). This can be expressed as:
  $ \begin{array}{l}
V = {x^2}\left( {\dfrac{{{c^2} - {x^2}}}{{4x}}} \right)\\
V = \dfrac{{{c^2}x}}{4} - \dfrac{{{x^3}}}{4}
\end{array} $
We will differentiate the above expression with respect to $ x $ . This can be expressed as
 $ \dfrac{{dV}}{{dx}} = \dfrac{{{c^2}}}{4} - \dfrac{{3{x^2}}}{4} $
 Now we will equate the above equation to zero to find the maximum or minimum value of $ V $ . This can be expressed as:
 $ \begin{array}{c}
\dfrac{{dV}}{{dx}} = 0\\
\dfrac{{{c^2}}}{4} - \dfrac{{3{x^2}}}{4} = 0\\
\dfrac{{{c^2}}}{4} = \dfrac{{3{x^2}}}{4}\\
{x^2} = \dfrac{{{c^2}}}{3}\\
x = \dfrac{c}{{\sqrt 3 }}\\
\end{array} $
 We will again differentiate $ \dfrac{{dV}}{{dx}} $ with respect to $ x $ .
 $ \begin{array}{l}
\dfrac{{{d^2}V}}{{d{x^2}}} = - \dfrac{{6x}}{4}\\
\dfrac{{{d^2}V}}{{d{x^2}}} = - \dfrac{{3x}}{2}
\end{array} $
We will find the value of $ \dfrac{{{d^2}V}}{{d{x^2}}} $ at $ \dfrac{c}{{\sqrt 3 }} $ for $ x $ .
 $ \begin{array}{l}
{\left[ {\dfrac{{{d^2}V}}{{d{x^2}}}} \right]_{x = \dfrac{c}{{\sqrt 3 }}}} = - \dfrac{{3\left( {\dfrac{c}{{\sqrt 3 }}} \right)}}{2}\\
{\left[ {\dfrac{{{d^2}V}}{{d{x^2}}}} \right]_{x = \dfrac{c}{{\sqrt 3 }}}} = - \dfrac{{3c}}{{2\sqrt 3 }}
\end{array} $
Since the value of $ \dfrac{{{d^2}V}}{{d{x^2}}} $ at $ \dfrac{c}{{\sqrt 3 }} $ for $ x $ is negative. Hence $ \dfrac{c}{{\sqrt 3 }} $ volume will be maximum.
We will find the value of $ h $ by substituting $ \dfrac{c}{{\sqrt 3 }} $ for $ x $ in equation (ii)
 $ \begin{array}{c}
h = \dfrac{{{c^2} - {{\left( {\dfrac{c}{{\sqrt 3 }}} \right)}^2}}}{{4\left( {\dfrac{c}{{\sqrt 3 }}} \right)}}\\
h = \dfrac{{2{c^2}}}{3} \times \dfrac{{\sqrt 3 }}{{4c}}\\
h = \dfrac{c}{{2\sqrt 3 }}
\end{array} $ …….(iii)
 We will substitute $ \dfrac{c}{{2\sqrt 3 }} $ for $ h $ and $ \dfrac{c}{{\sqrt 3 }} $ for $ x $ in the equation (i)
 $ \begin{array}{l}
V = {\left( {\dfrac{c}{{\sqrt 3 }}} \right)^2}\left( {\dfrac{c}{{2\sqrt 3 }}} \right)\\
V = \dfrac{{{c^3}}}{{6\sqrt 3 }}
\end{array} $
Hence, it is proved.

Note: On double differentiating the volume if the value comes negative then it represents maxima but if the value comes out positive then represents minima. In our solution the value of double differential is negative, hence it denoted maxima for that particular value.