Question

An iron sphere weighs 10N and rests in a V shaped trough whose sides from an angle $ + 6V,{(1/30)^{3/2}}$. The net force exerted by the walls on the sphere in case as shown in figure is:

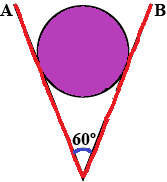
A. 0 N
B. 10 N
C. $\dfrac{{10}}{{\sqrt 3 }}$
D. 5N

Answer 1

Hint:- Here in this question we have to resolve the forces into $\cos \theta $ and $\sin \theta $. After resolving the two forces which are exerted by the wall on the ball add the two forces. Put the value of given angle, one would be able to find the net force exerted.

Complete step-by-step solution:-
 Resolve and add the forces.

The forces would become;
$N\cos \theta = - N\cos \theta $;
Now, for the net force add the two forces together,
\[{F_{Net}} = N\cos \theta + N\cos \theta \] ;
In place of\[{F_{Net}}\]put the force exerted by the ball which is 10 N.
\[10 = N\cos \theta + N\cos \theta \]
Since the two forces are together add the two forces.
$2N\cos \theta = 10N$;
Take “2” to the RHS and divide by 10N.
$N\cos \theta = \dfrac{{10N}}{2}$;
Here, find the value of N
$N\cos \theta = 5N$;
Solve the equation and put the value of the given angle,
$\cos \theta = \cos 60 = \dfrac{1}{2}$ ;
Put the above value into the equation;
$N = 5 \times 2N$;
The net force comes out to be:
$N = 10N$;
Final Answer: Option “2” is correct. The net force exerted by the walls on the sphere is 10 N.

Note:- Here make sure to make the diagram properly and resolve the forces. Here we have considered only \[N\cos \theta \]because that is the only force which is acting on the ball; the vertical force \[N\sin \theta \] is not acting on the ball so it is not considered.