Question

An iron core shaped as a tire with a mean radius $R = 250mm$ supports a winding with the total number of turns $N = 1000$ . The core has a cross-cut of width $b = 1.00mm$ . With a current $I = 0.85A$ flowing through the winding, the magnetic induction in the gap is equal to $B = 0.75T$ . Assuming the scattering of the magnetic flux at the gap edges to be negligible, find the permeability of iron under these conditions.

Answer 1

Hint: - First we will draw the diagram for the iron core, then by applying Ampere circuital law, we can find an equation for straight-line relating magnetic field $B$ and magnetic field strength $H$ . Once we get the equation, we can find the value of permeability of iron using the value of $B$ and $H$ .

Formula used:
$\oint {H.dl = NI} $
$H = \dfrac{B}{\mu }$

Complete step-by-step solution:
The iron core which is given here can be shown as follows

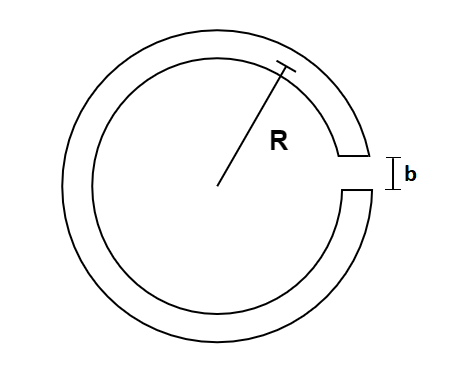
On the given core there is winding having $1000$ turns and current of $0.85A$ .
Now the magnetic field strength can be given by ampere circuital law which states that the line integral of the magnetic field strength for the material is equal to the current flowing through it.
$\oint {H.dl = NI} $
Here $H$ is magnetic field strength, $dl$ is the infinitesimal length, $N$ is the number of turns and $I$ is the current.
Now if we apply the line integral on the core we get
$H\left( {2\pi R - b} \right) + H'\left( b \right) = NI$ ................... $\left( 1 \right)$
$H$ is the field strength of the ring excluding the cross-cut part (therefore $b$ is subtracted from $2\pi R$ ) and $H\prime $ is field strength from the cross-cut part. Now the cross-cut part is in Vacuum, therefore, $H\prime $ can be given as,
$H' = \dfrac{B}{{{\mu _0}}}$
where ${\mu _0}$ is the permeability in free space.
Substituting this in the equation $\left( 1 \right)$ , we get
$H\left( {2\pi R - b} \right) + \dfrac{B}{{{\mu _0}}}\left( b \right) = NI$
$ \Rightarrow \dfrac{B}{{{\mu _0}}}b = NI - H\left( {2\pi R - b} \right)$
On further solving the equation we get,
$ \Rightarrow B = \dfrac{{{\mu _0}}}{b}\left[ {NI - H\left( {2\pi R - b} \right)} \right]$
Now we have given the values of $R$, $b$, $N$ and $I$ which are
$R = 250mm = 0.25m$ , $b = 1.00mm = 0.001m$ , $N = 1000$ and $I = 0.85A$
Substituting all these values
$B = \dfrac{{1.26 \times {{10}^{ - 6}}}}{{0.001}}\left[ {\left( {1000} \right)\left( {0.85} \right) - H\left( {2\left( {3.14} \right)0.25 - 1} \right)} \right]$
$ \Rightarrow B = 1.26 \times {10^{ - 3}}\left[ {850 - H\left( {1.57 - 0.001} \right)} \right]$
On further solving the equation we get,
$B = 1.071 - 0.0019H$ .......................$\left( 2 \right)$
On putting the value $B = 0.75T$ we get,
$0.75 = 1.071 - 0.0019H$
$ \Rightarrow 0.0019H = 1.071 - 0.75$
$ \Rightarrow H = 168.94A/m$
Now the relation between $H$ and $B$ is given by the formula
$\mu = \dfrac{B}{H}$
where $\mu $ is the permeability of the material. Hence by using the formula we can find the permeability of iron rings.
Now substituting the value of $H$ and $B$, we get
$\mu = \dfrac{{0.75}}{{168.94}}$
$ \Rightarrow \mu = 4.439 \times {10^{ - 3}}N{A^{ - 2}}$
Hence, the permeability of iron under these conditions will be $4.439 \times {10^{ - 3}}N{A^{ - 2}}$ .

Note: Mostly permeability is measured in henry per meter i.e. $H/m$ but to dodge misperception between magnetic field strength and henry we used another unit of permeability. Also, note here we calculated the permeability of material and not the relative permeability which can be given by the ratio of permeability of a material to the permeability in free space.