Question

An ionized gas contains both positive and negative ions. If it is subjected simultaneously to an electric field along the $+x-\text{direction}$ and a magnetic field in the $+z\text{ direction}$, then
A. Positive ions deflect towards the +y-direction and the negative ions towards the -y direction.
B. All ions deflect towards the +y direction.
C. All ions deflect towards the -y direction.
D. Positive ions deflect towards the -y-direction and the negative ions towards the +y direction.

Answer 1

Hint: We know that when an electric field is applied across a medium, the ions in the medium will be attracted or repelled depending on the nature of the charge of an ion. If the field is applied in the $+x-\text{direction}$ then negative ions will be drifted towards the $-x-\text{direction}$ and the positive ion will be drifted towards the $+x-\text{direction}$. Due to this movement, the ions attains a velocity. We know that a charged particle moving with a velocity v in a magnetic field will experience a force that is perpendicular to both the direction of the magnetic field and the direction of velocity.

Formula Used:
The force acting on a charged particle q moving with a velocity v in a magnetic field B is given by,
\[\overrightarrow{F}=q\left( \overrightarrow{v}\times \overrightarrow{B} \right)\]

Complete step by step answer:

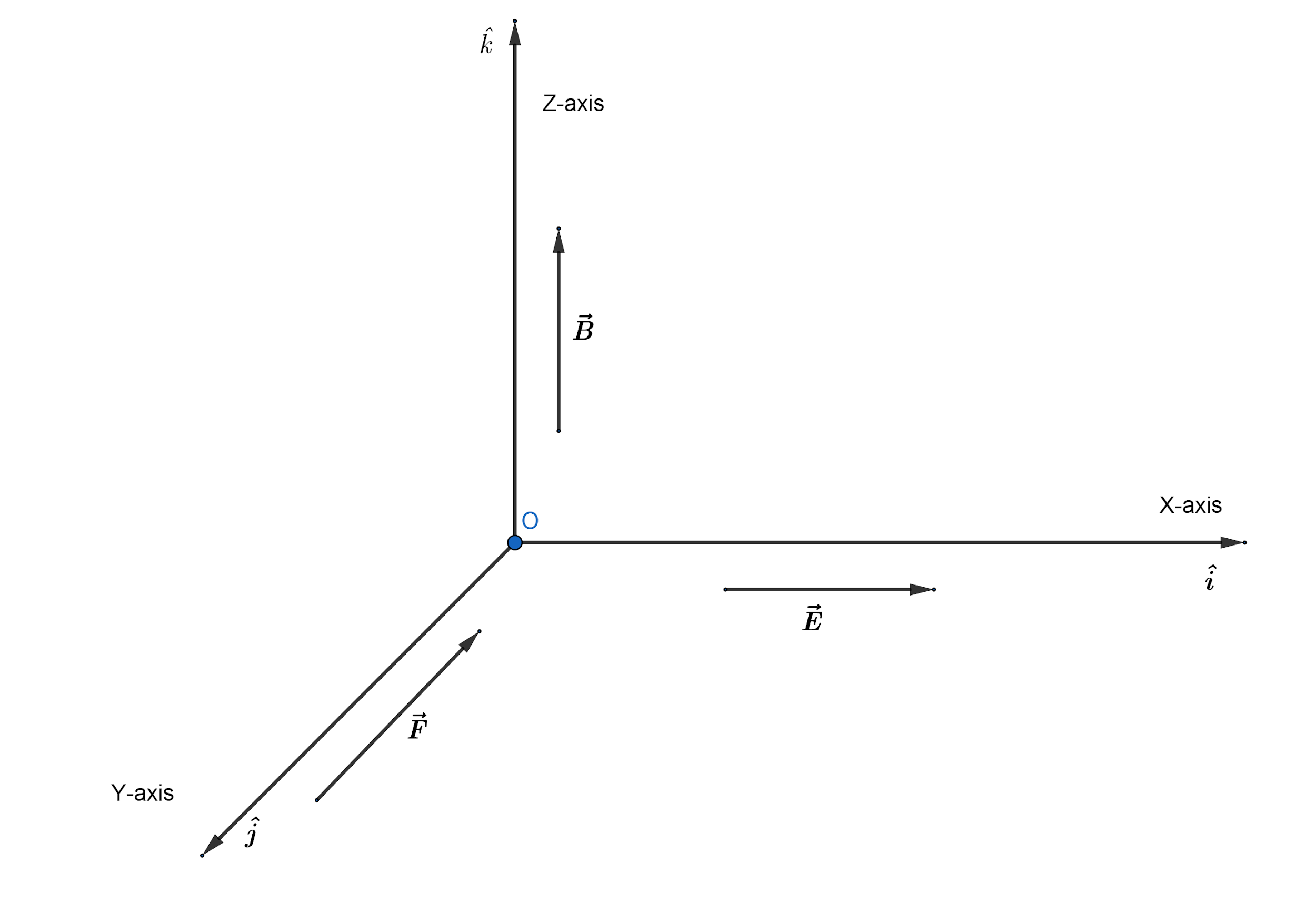
The ionized gas in the question contains both positive and negative ions. So, when an electric field is applied across the $+x-\text{direction}$ the positive ions will be drifted towards the positive side, and the negative ions will be drifted towards the $-x-\text{direction}$. Let $v$ be the velocity with which the ions (both positive and negative) move. So since a magnetic field is present in the $+z\text{ direction}$ the ions will experience a force given by the formula,
\[\overrightarrow{F}=q\left( \overrightarrow{v}\times \overrightarrow{B} \right)\]
Where
q is the charge of the ions.
B is the magnetic field.
So, when a positive ion moving in the $+x\text{ direction}$ goes through a magnetic field which is in the $+z\text{ direction}$, then the force acting on the ion is,
\[\overrightarrow{F}=q\left( \overrightarrow{v}\times \overrightarrow{B} \right)\]
\[\overrightarrow{F}=q\left( v\hat{i}\times B\hat{k} \right)\]
Where $\hat{i}\text{ and }\hat{k}$ are unit vectors along x and z axes, respectively.
So, we can write,
\[\overrightarrow{F}=qvB\left( \hat{i}\times \hat{k} \right)\]
\[\overrightarrow{F}=qvB\left( -\hat{j} \right)\text{ }\left( \because \hat{i}\times \hat{k}=-\hat{j} \right)\]
So, the force on the positive ion will be along the $-y-\text{direction}$.
So, when a negative ion moving in the $-x\text{ direction}$ goes through a magnetic field which is in the $+z\text{ direction}$, then the force acting on the ion is,
\[\overrightarrow{F}=-q\left( \overrightarrow{v}\times \overrightarrow{B} \right)\]
\[\overrightarrow{F}=-q\left( -v\hat{i}\times B\hat{k} \right)\]
Where $-\hat{i}\text{ and }\hat{k}$ are unit vectors along the negative x and positive z axes, respectively.
So, we can write,
\[\overrightarrow{F}=qvB\left( \hat{i}\times \hat{k} \right)\]
\[\overrightarrow{F}=qvB\left( -\hat{j} \right)\text{ }\left( \because \hat{i}\times \hat{k}=-\hat{j} \right)\]
So, the force on the negative ion will be along the $-y-\text{direction}$.
So, both the negative and positive charges will be deflected along the negative y-direction.
So, the answer to the question is (C).

Note: This problem can also be solved using Fleming’s left-hand rule, which states that “ if a current-carrying conductor is placed in a magnetic field which is perpendicular to each other then the current-carrying conductor experiences a force perpendicular to both magnetic field and current direction so if we stretch the thumb, forefinger and middle finger in such a way that they are mutually perpendicular to each other. Then if the middle is directed along the direction of the current, the forefinger towards the magnetic field, then the thumb will point towards the direction of the force.”
So, in the question, due to the movement of charge carriers there will be current along the $+x-\text{direction}$, and there is a magnetic field along the $+x-\text{direction}$ then from the left hand we can understand the force is along the –y-direction. So, all the ions should be drifted in that direction.