Question

An interference is observed due to two coherent sources ‘A’&’B’ separated by a distance of $\text{4 }\lambda$ along the y-axis where $\lambda$ is the wavelength of the
source. A detector D is moved on the positive x-axis. The number of points on the x-axis excluding the points, x=0 & x=$\infty $ at which maximum will be observed is

A. Three
B. Four
C. Two
D. Infinite

Answer 1

Hint: To know at which point maxima will be observed, we need to find all the points. Now, to find the points we will construct a diagram or figure which can elaborate the question for better clarity. After constructing the diagram, we can find all the points of maxima, and then remove those points which are given in question.

Complete step-by-step solution:
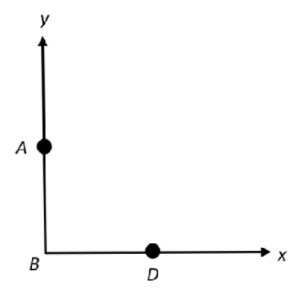
First of all let us construct a rough figure to get an idea for proceeding further,
Now, in the diagram,
AB=$\text{4 }\lambda$ (Given in the question)

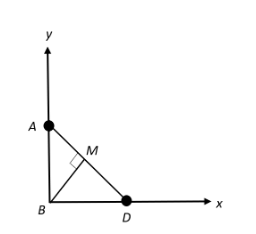
Now, let us consider a triangle ABD,
$\Rightarrow {{\left( \text{AD} \right)}^{\text{2}}}\text{=}{{\left( \text{AB}
\right)}^{\text{2}}}\text{+}{{\left( \text{BD} \right)}^{\text{2}}}$
$\Rightarrow {{\left( \text{AM+MD} \right)}^{\text{2}}}\text{=}{{\left( \text{AB}
\right)}^{\text{2}}}\text{+}{{\left( \text{BD} \right)}^{\text{2}}}$ -----equation(1)
Here, AM is the path difference,
Therefore, AM=BD=${{\text{x}}_{\text{n}}}$
Now, let us put the values in equation (1),
$\Rightarrow {{\left( \text{n }\lambda\text{ +}{{\text{x}}_{\text{n}}}
\right)}^{\text{2}}}\text{=}{{\left( \text{4 }\lambda \right)}^{\text{2}}}\text{+}{{\left(
{{\text{x}}_{\text{n}}} \right)}^{\text{2}}}$
$\Rightarrow {{\text{x}}_{\text{n}}}\text{=}\dfrac{\text{16}{{\lambda}^{\text{2}}}\text{-
}{{\text{n}}^{\text{2}}}{{\lambda}^{\text{2}}}}{\text{2n }\lambda}$ - ------equation (2)
Now, we will put the value of $n$ as, $n=1,2,3,4$.. in the above equation (2).
$\Rightarrow {{\text{x}}_{\text{1}}}\text{=}\dfrac{\text{16}{{\lambda}^{\text{2}}}\text{-
}{{\lambda}^{\text{2}}}}{\text{2 }\lambda}=7.5\lambda$
$\Rightarrow {{\text{x}}_{2}}\text{=}\dfrac{\text{16}{{\lambda}^{\text{2}}}\text{-
4}{{\lambda}^{\text{2}}}}{\text{4 }\lambda}=3\lambda$
$\Rightarrow {{\text{x}}_{3}}\text{=}\dfrac{\text{16}{{\lambda}^{\text{2}}}\text{-
9}{{\lambda}^{\text{2}}}}{\text{6 }\lambda}=\dfrac{7}{6}\lambda$
$\Rightarrow {{\text{x}}_{4}}=0$
Hence, the number of points where maxima is observed is 3. Therefore, we conclude that the final answer is option A.), which is A. three

Note: There is no particular formula for this question, applying which we can get the answer, so we will be required to construct the figure and label it accordingly and then only proceed further to get the answer of this question. At last, after getting all the maxima points, don’t forget to remove the point where it is zero and infinity, as given in the question.