Question

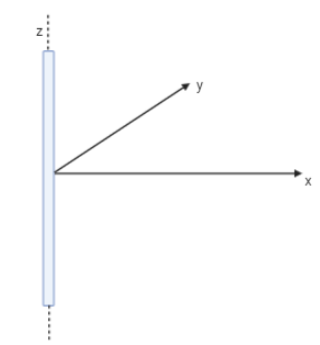
An infinitely long wire is kept along the z-axis from $z = -\infty$ to $z= +\infty$, having uniform linear charge density $\dfrac{{10}}{9}nC/m$ . The electric field E at point $\left( {6cm,8cm,10cm} \right)$ will be:

A. $\left( {160i + 120j + 200k} \right)N/C$
B. $\left( {200k} \right)N/C$
C. $\left( {160i + 120j} \right)N/C$
D. $\left( {120i + 160j} \right)N/C$

Answer 1

Hint:We will calculate the electric field at any point from the wire and the magnitude of electric field along x-axis is calculated by the product of this electric field and cosine of the angle formed between them. Also, the electric field along the y-axis is obtained by multiplying the sin value with this electric field.

Complete step by step answer:
A wire of infinite length is kept along z-axis from the coordinate $z = - \infty $ to $z = + \infty $ and its linear charge density (λ) is $\dfrac{{10}}{9}nC/m$ . A linear charge density is defined as charge carried by the wire per unit length. The effect of the electric field due to this wire at the z-axis is zero as the wire is placed along the z-axis and it extends till infinity from both the negative and positive side of the axes. Hence, the value of the electric field at z-coordinate i.e.,10 cm is zero.

The electric field $\left( E \right)$ at any particular point from the wire is $\dfrac{\lambda }{{2\pi r{ \in _0}}}$ when the wire is of very large length i.e., infinite length.
$E = \dfrac{\lambda }{{2\pi r{ \in _0}}}$ where r is the distance of point from z-axis.
$\Rightarrow E = \dfrac{{\dfrac{{10}}{9} \times {{10}^{ - 9}}}}{{2 \times \dfrac{{22}}{7} \times 10 \times {{10}^{ - 2}} \times 8.854 \times {{10}^{ - 12}}}}\left[ {1nC = {{10}^{ - 9}}C,1cm = {{10}^{ - 2}}m} \right]$
$\Rightarrow E = \dfrac{{{{10}^{ - 8}}}}{{2 \times \dfrac{{22}}{7} \times 9 \times 8.854 \times {{10}^{ - 13}}}}$
$\Rightarrow E = \dfrac{{{{10}^5}}}{{500.88}}$
$\Rightarrow E = 0.0019964 \times {10^5}i.e.,199.64N/C$
$\Rightarrow E = 200N/C\left( {rounded{\text{ }}of{\text{ }}value} \right)$
The value of electric field along x-axis $\left( {{E_x}} \right)$ is $E\cos \theta $ and electric field along y-axis $\left( {{E_y}} \right)$ is $E\sin \theta $ .
Thus, ${E_x} = E\cos \theta $
${E_x} = 200 \times \dfrac{6}{{10}}\left[ {\cos \theta = \dfrac{{base}}{{hypotenuse}}} \right]$
$\Rightarrow{E_x} = 120N/C$
$\Rightarrow{E_y} = E\sin \theta \left[ {\sin \theta = \dfrac{{height}}{{hypotenuse}}} \right]$
$\Rightarrow{E_y} = 200 \times \dfrac{8}{{10}}$
$\therefore{E_y} = 160N/C$

Therefore, option D is correct i.e., (120 i+160 j)N/C where i represent x-axis and j represent y-axis.

Note:The wire is of infinite length and it is kept along the z-axis. So, the value of the electric field at any point lying in the z-axis is negligible. The magnitude of electric field depends on the distance of point from the line of charge i.e., wire and it is inversely proportional to the distance of the point from the wire.