Question

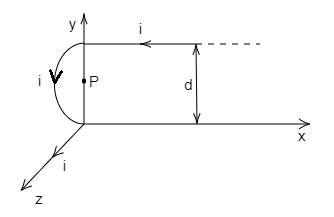
An infinitely long conductor carrying the current $i$ with a semiconductor loop in the $x - y$ plane and two straight parts. One parallel to $x$ axis and another coinciding with $z$ axis. What is the magnetic field at the centre $P$ of the semiconductor loop?

Answer 1

Hint
By using the formula of the magnetic field of a straight wire carrying the current, the magnetic field is determined. Here the current is passed in three wires, so the three magnetic fields are determined and by adding the three magnetic fields, the magnetic field at the centre $P$ is determined.
The magnetic field of a straight wire carrying the current is given by,
$\Rightarrow B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}$
Where, $B$ is the magnetic field, ${\mu _0}$ is the permeability of free space, $I$ is the current and $r$ is the distance.

Complete step by step answer
The magnetic induction at $P$ due to the current through straight part of the conductor parallel to $x$ axis is, then
$\Rightarrow {B_1} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}$
The magnetic field act along $z$ axis, then
$\Rightarrow {\vec B_1} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}\hat k\,.................\left( 1 \right)$
The magnetic field induction at $P$ due to current through the semi-circular loop in $x - y$ plane is, then
$\Rightarrow {B_2} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I\pi }}{r}$
The magnetic field act along $z$ axis, then
$\Rightarrow {\vec B_2} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I\pi }}{r}\hat k\,.................\left( 2 \right)$
The magnetic field induction at $P$ due to current through the straight part of the conductor coinciding with $z$ axis is, then
$\Rightarrow {B_3} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}$
The magnetic act outwards, so it is negative, then
$\Rightarrow {\vec B_3} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}\left( { - \hat i} \right)\,..................\left( 3 \right)$
The total magnetic field at $P$ is,
$\Rightarrow \vec B = {\vec B_1} + {\vec B_2} + {\vec B_3}$
By substituting the equation (1), equation (2) and equation (3) in the above equation, then the above equation is written as,
$\Rightarrow \vec B = \left( {\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}\hat k} \right) + \left( {\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I\pi }}{r}\hat k} \right) + \left( {\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}\left( { - \hat i} \right)} \right)$
By taking the term $\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}$ as a common term and take this term outside from the equation, then the above equation is written as,
$\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}\left[ {\hat k + \pi \hat k - \hat i} \right]$
Then the above equation is also written as,
$\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}\left[ {\left( {1 + \pi } \right)\hat k - \hat i} \right]$
Thus, the above equation shows the total magnetic field at the centre $P$.

Note
In every vector equation the unit vector is multiplied, so that the unit vector $\hat k$ is multiplied with the equation (1) and the equation (2) and the unit vector $\hat i$ is multiplied with the equation (3). The current is passing through the three wires, so the magnetic field is produced in both the three wires. By adding the three equations, the total magnetic field is determined.