Question

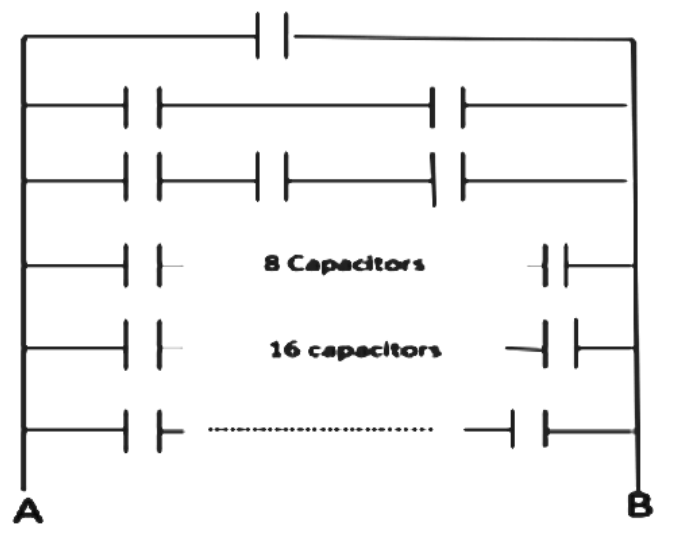
An infinite number of identical capacitors, each of capacitance $1\mu F$ are connected as shown in the figure. Then the equivalent capacitance between A and B is:

$\left( A \right)1\mu F$
$\left( B \right)2\mu F$
$\left( C \right)\dfrac{1}{2}\mu F$
$\left( D \right)\infty $

Answer 1

Hint: Current flowing through the capacitors is the same for all the capacitors when the capacitor is connected in series. Then each capacitor will have the same amount of electrical charge. In parallel connection the voltage is the same for all capacitors connected parallels. Apply this logic to find the Charge in the circuit.

Formula used:
$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + ....... + \dfrac{1}{{{C_n}}}$

Complete step by step answer:
Capacitor is a component that has the capacity to store the energy. It is in the form of electrical charge producing a potential difference across its plates. Electrons flowing onto the plates are known as charging of capacitors. The potential difference depends on the number of charges present on the plates of the capacitor.
If the DC source is one in a resistance containing circuit, then the current will attain its maximum steady value in zero-time interval. A resistor circuit containing both inductor and capacitor, the current will take some time to attain its maximum peak value. If the battery is removed from the circuit which is having a capacitor or an inductor, then the current takes some time to decay to zero value.
Current flowing through the capacitors is the same for all the capacitors when the capacitor is connected in series. Then each capacitor will have the same amount of electrical charge. In parallel connection the voltage is the same for all capacitors connected parallels. Apply this logic to find the capacitance of the circuit.
Capacitance for infinite capacitance when connected in series,
$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + ....... + \dfrac{1}{{{C_n}}}$
We get ${C_1} = {C_2} = ....... = {C_n}$
Capacitance equivalent is given by,${C_{eq}} = \dfrac{C}{n}$
For the first row,
$ \Rightarrow {C_A} = C$
For the second row,
$ \Rightarrow {C_B} = \dfrac{C}{2}$
For the third row,
$ \Rightarrow {C_c} = \dfrac{C}{4}$
Then the final capacitance is,
$ \Rightarrow {C_{final}} = {C_A} + {C_B} + ....... + {C_\infty }$
$ \Rightarrow {C_{final}} = C + \dfrac{C}{2} + ...... + \dfrac{C}{\infty }$
From geometric progression
$ \Rightarrow {C_{final}} = \dfrac{C}{{1 - \dfrac{1}{2}}} = 2C = 2\mu F$

Hence, the correct answer is option (B).

Note: Electron flowing onto the plates is known as charging of capacitor. The potential difference depends on the number of charges present on the plates of the capacitor. : If the battery is removed from the circuit which is having a capacitor or an inductor, then the current takes some time to decay to zero value.