Question

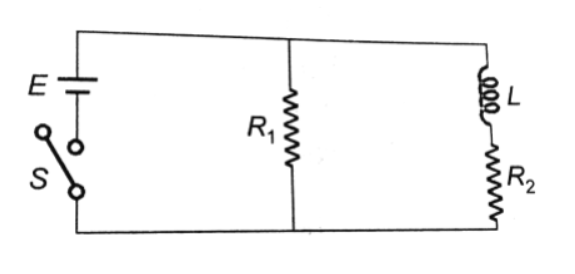
An inductor of inductance L = 400 MH and resistors of ${R_1}\, = \,2\Omega $ and ${R_2}\, = \,2\Omega $ are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t = 0. The potential drop across L as a function of time is –

A. ${12_e}^{5t}V$
B. $\dfrac{{12}}{t}{e^{3t}}V$
C. $6\left( {1\, - \,e\dfrac{{ - t}}{{0.2}}} \right)V$
D. $6{e^{ - 5t}}V$

Answer 1

Hint - As we know that two parts of the circuit are in parallel with the battery, we will first study about potential drop and then coming on the solution, we will break the circuit and with the help of diagrams, we can easily calculate the Potential drop and hence, getting the solution for our question.

Complete step-by-step answer:
Potential drop –
Potential drop, also known as voltage drop of a circuit, is the measure of how much voltage (supplied by the sources of voltage) is reduced by the passive elements (such as resistors, capacitor or inductors). In simple words, it is the amount of voltage lost due to resistances present in the circuit.
Voltage drop or Potential drop takes place when current flows from higher potential to lower potential across a passive element. If the potential is the same across both the ends, then there is no voltage drop across it.

Now, we have
$
  {R_1}\, = \,2\Omega ,\,{R_2}\, = \,2\Omega ,\,E\, = \,12V\,and\,L\, = \,400MH\, = \,0.4H \\
    \\
$
We know that two parts of the circuit are in parallel with the battery applied.
So, we are breaking the circuit-

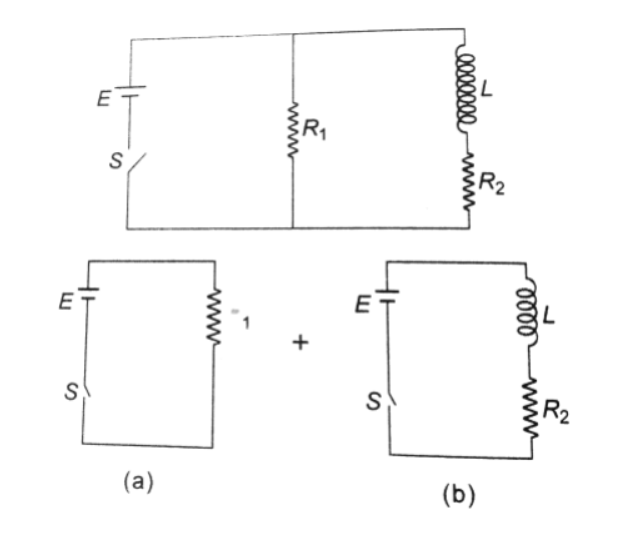
Figure b is a simple L – R circuit, which has a time constant
${\tau _L}$ = $\dfrac{L}{{{R_2}}}\, = \,\dfrac{{0.4}}{2}\, = \,0.2s$
And steady state current

As we know switch S is closed at time t = 0, then current in the circuit at any time t
$i\left( t \right)\,\, = \,\,\left( {1\, - \,{e^{\dfrac{{ - t}}{{{\tau _L}}}}}} \right)$
$i\left( t \right)\,\, = \,\,6\left( {1\, - \,{e^{\dfrac{{ - t}}{{0.2}}}}} \right)$
$ = \,6\left( {1\, - \,{e^{ - 5t}}} \right)\,\, = \,\,i$
Hence Potential drop across L at any time t is
$
  V\, = \,\left| {\left. {L\dfrac{{di}}{{dt}}} \right|} \right.\, = \,L\left( {30{e^{ - 5t}}} \right)\, = \,\left( {0.4} \right)\,\left( {30} \right){e^{ - 5t}} \\
  \, = \,V\, = \,12{e^{ - 5t}}volt \\
$

Note – In terms of measurement, Potential drop just means the voltage difference between the two points in a circuit. In simple words, it is the amount of voltage lost due to resistances present in the circuit. The total of all the potential drop in any circuit is equal to the value of potential source of the circuit driving it.